Exponential Functions
It's common to confuse a function that has an exponent (ex. ) with an exponential function (ex. ), but they are different. An exponential function means that the x-value is the exponent and the base is the constant. Let's take a closer look at exponential functions.
The basics of exponential functions
The "basic" exponential function is with "a" being a positive constant and "x" being a variable. An exponential function is a function that increases (if ) or decreases (if ) exponentially.
A simple example of an exponential function is , which has the following graph:
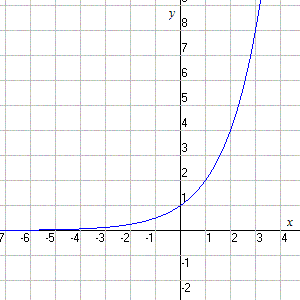
The graph shows a curved line for the slope, which represents a rapid increase, as opposed to a straight line for the slope of a linear function.
Domain and range of exponential functions
You can't discuss functions without mentioning domain and range. The domain of a function is the set of input or -values for which the function is defined, while the range is the set of all the output or -values that the function takes.
The domain and range of exponential functions are slightly different than those of functions. The domain of an exponential function is all real numbers. And the range of an exponential function of the form is all real numbers greater than zero (all positive real numbers).
For exponential functions, and
For the exponential function , to have only real values a must be greater than zero. Why? If , some outputs might instead be complex numbers.
As for why , consider that if , y will always equal 0, for all . You can see this below for :
means
means
means
This will make the function a constant function (which means the range won't change no matter which member of the domain is used).
This is also a reason that . You can see below that for , y remains constant no matter which x is used:
means
means
means
means
When graphed, gives you a horizontal line at .
Graphing exponential functions
Now that we've gone over the basics of the exponential function, let's take a look at how to graph an exponential function like . It's good to start by creating a table that allows you to clearly see the variables:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Next, plot the points on a graph:

Here are some things to note about this graph:
- The y-intercept is 1 no matter the value of a because in this case, will always result in .
- The graph approaches the x-axis asymptotically (it approaches arbitrarily close without crossing it) as x goes to negative infinity.
- The graph is always positive (never zero or negative). In other words, the data rises from left to right.
Now, let's say that you want to adjust the base of the equation by replacing the 2. Below, you can see graphs of and :
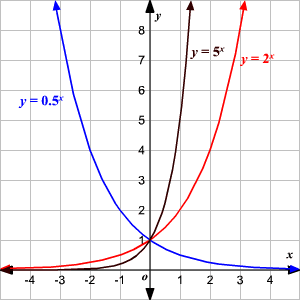
(Note: represents exponential growth and represents exponential decay.)
For the above graph, adjusting the base changes the shape of the graph. In the case of , the graph changes from increasing to decreasing. It's good to note that the y-intercept still remains 1 no matter the value of a.
Now, let's look at what it would take to shift this graph. Suppose you replace with . This means that the graph translates (or in this case, 3) units to the left:

If you replace with (which is the same as adding k to the right side), you will translate the graph k (or 4) units up:

With an equation like , you shift the exponential function k units up and h units to the right. For example, take a look at a graph of the equation :

Graphing this equation starts with the "basic" exponential graph . Then, you'll shift the graph three units to the right and two units up.
Practice questions on exponential functions
a. True or false: The following is an exponential function .
False. In order for a function to have all real numbers, a must be restricted to all positive numbers.
b. What is the domain of an exponential function?
The domain of an exponential function is all real numbers.
c. True or false: For is an exponential function.
False. This is a constant function.
d. If for , you replace x with x+h so that the function now reads , what happens to the graph?
The graph shifts h units to the left.
e. If for , you replace y with so the function now reads , what happens to the graph?
The graph shifts k units up.
f. If you graph then write an equation like , what happens to the graph?
You shift the graph 5 units to the right and 3 units up.
Topics related to the Exponential Functions
Exponential to Logarithmic Form
Flashcards covering the Exponential Functions
Practice tests covering the Exponential Functions
College Algebra Diagnostic Tests
Get help learning about exponential functions
At first glance, exponential functions can be a bit confusing, particularly if your student is accustomed to seeing x as the base of an equation as opposed to the exponent. Your student might want to become more familiar with the domain and range of an exponential function or learn more about how an exponential function is graphed. Fortunately, there are fantastic tutors available to assist your student. Tutoring can help students who are doing well in math already, too. Math tutors are great for students of all abilities. If you want to find out more about the benefits of having your student take part in private math tutoring sessions, don't hesitate to reach out to the Educational Directors at Varsity Tutors to get your student started today.
- Pedology Tutors
- Montana Bar Exam Courses & Classes
- Finnish Tutors
- Super Smash Bros. Melee Tutors
- AFOQT - Air Force Officer Qualifying Test Courses & Classes
- LMSW Exam Test Prep
- Accelerated Writing and Composition Tutors
- CTRS - A Certified Therapeutic Recreation Specialist Test Prep
- Korean Lessons
- NNAT Test Prep
- Medieval Literature Tutors
- Madden NFL 18 Tutors
- TEAS Courses & Classes
- OAE - Ohio Assessments for Educators Courses & Classes
- AFSP - Annual Filing Season Program Courses & Classes
- NAPLEX Test Prep
- Nebraska Bar Exam Courses & Classes
- Insurance License Tutors
- AP Calculus AB Tutors
- New Hampshire Bar Exam Courses & Classes