Rational Functions
Occasionally, terminology in mathematics can be somewhat deceptive. Take "rational functions" as an example – they may not be as straightforward as the name suggests, and they can pose certain challenges. However, by breaking down the concept step by step, we can develop a strong understanding of rational functions. So, what exactly are they? How do they function? What insights can they offer us about mathematics, and how can we apply this knowledge to tackle mathematical problems? Let's dive in and explore:
The definition of a rational function
A rational function is a function that can be defined by a rational fraction. So what exactly is a rational fraction?
A rational fraction is a fraction with a polynomial for both its numerator and denominator. We can also call this a "ratio" of two polynomials.
Here are a few examples:
As we can see, all of these fractions have polynomials as their numerators and denominators.
Note that the denominator cannot be equivalent to zero. Why? Because this would make the entire rational function "undefined." We can write a rational function with the following formula:
A function can only be called a rational function if it can take the form of . In this formula, and must both be polynomials. Another important rule: cannot equal zero. As previously mentioned, this would make the function undefined (more on this later).
Rational functions and hyperbolas
You might recall that when we graph a function in its simplest possible form, this is known as a "parent function" or "parent graph." The simplest way to express a rational function is . So what does this look like when we graph it? Take a look:
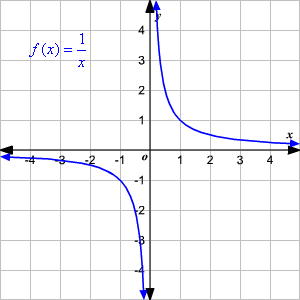
As we can see, this parent function adopts a very specific form when graphed. We call this a "hyperbola." Defined as an "open curve with two branches" or "the intersection of a plane with both halves of a double cone," a hyperbola always has two pieces.
Graphing the function is just one of many ways to produce a hyperbola. We also see hyperbolas when we track the path of a shadow created by a sundial.
The word "hyperbola" comes from a Greek word that means "excessive" or "overthrown." The word "hyperbole" is also related to the same root word. The Greeks discovered hyperbolae (the plural form of hyperbola) when studying conic sections.
Graphing hyperbolae helps us understand one of the most important lessons associated with this subject: Notice how both of the branches never intersect with the origin . This is because -- as we have already established -- the polynomial cannot equal zero.
This lesson also shows us that the domain and range of the function are the set of all real numbers except zero. The branches extend infinitely, but they can never intersect with zero coordinates.
We can write this as:
Domain:
Range:
With that said, a rational function does not necessarily need to be centered on the origin. It may be centered around some other point.
Rational functions and excluded value
The concept of "excluded value" is another important lesson as we cover rational functions.
An excluded value is an x-value that makes the entire function undefined. We call them "excluded values" because they are always "excluded" from the domain of our rational function.
Consider the following function:
What is the excluded value of this function? In other words, which x value would make this function undefined?
The excluded value of this function is:
Why? Because if , then the denominator becomes zero -- and the function is now undefined. But if we put in values really close to 3, then we get outputs that are larger and larger approaching infinity.
In this situation, we can say that the domain of the function is the set of all real numbers except -3.
Rational functions and asymptotes
The concept of an "asymptote" is also very important in the context of rational functions. Although this word might sound quite complicated, the concept is very simple:
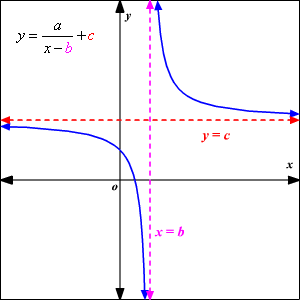
An asymptote is the line that the graph of the function approaches but never touches. A function may have both vertical and horizontal asymptotes. Together, these two lines form a cross. Let's take a look at how this works:
If we graph the most basic parent function , then finding the asymptotes is easy. Why? Because the asymptotes are simply the x and y-axes.
But in this particular graph, we see something different. The hyperbola is not centered around the origin, and instead, it takes the form of .
In this case, its vertical asymptote is the excluded value . Its horizontal asymptote, on the other hand, is . This graph shows the importance of finding the excluded value.
Applications of rational functions
But why are rational functions important? Why do we need to learn about them, and when might they be important in everyday life? Rational functions have many applications:
- Numerical analysis: Rational functions may be especially useful in the world of numerical analysis -- especially when it comes to interpolation and approximation of functions. Both interpolation and approximation are forms of estimation, and they allow us to find new data points based on the range of a discrete set of known data points. One of the best-known examples of this is the Padé approximant, which gives the "best" approximation of a function near a specific point. This method has become especially popular in the world of computer science.
- Science: Rational functions may prove useful in many scientific fields, including physics, chemistry, biochemistry, electronic circuitry, aerodynamics, medicine, wave functions, optics, acoustics, and many others. Once again, they allow us to approximate complex equations -- allowing us to solve many complex problems in these fields.
- Signal Processing: Rational functions can also be quite useful in the field of signal processing, which deals with modifying and synthesizing signals associated with sound, images, seismic fields, scientific measurements, and many others. People use rational functions when working on electronic music, video processing, seismology, and many other tasks.
Graphing rational functions
When graphing rational functions, it's important to follow a few simple steps:
1. Find the asymptotes of the rational function. This will allow you to check the accuracy of your graph -- and it helps you find the excluded values. Note that in some cases, the rational function will have no asymptotes.
2. Draw the asymptotes of the rational function before graphing the actual function itself. This will provide us with an "outline" that makes it easier to graph our function. It also shows us the exact coordinates where the function cannot exist.
3. Find the x and y-intercepts of the rational function. Once again, there may be no x and y-intercepts when we deal with some rational functions.
4. Find the values of y for several different values of x. You do not need to find all corresponding coordinates (as this would be impossible), but start with a handful to get the general shape of the graph.
5. Plot the points of these coordinates and connect them using a smooth, curved line. Make sure not to intersect with the asymptotes.
Topics related to the Rational Functions
Domain and Range of Rational Functions
Flashcards covering the Rational Functions
Practice tests covering the Rational Functions
Pair your student with a tutor who understands rational functions
When you take the time to really break things down, rational functions really aren't so complicated. Here's the problem: Your student might not be given enough time or attention in class to truly feel confident about rational functions and related concepts. Fortunately, Varsity Tutors pairs your student with a knowledgeable and fully-vetted tutor -- giving your student all the time they need to ask questions and voice concerns in a personalized, 1-on-1 environment. Tutoring can be beneficial for students of all ability levels, so get in touch with our Educational Directors today to get your student started.
- iOS Development Tutors
- ABIM Exam - American Board of Internal Medicine Courses & Classes
- Louisiana EOC Courses & Classes
- CFA Test Prep
- Series 82 Courses & Classes
- California Proficiency Program (CPP) Courses & Classes
- English Literature Tutors
- Series 4 Test Prep
- LSAT Logical Reasoning Tutors
- 8th Grade Homework Tutors
- SAT Subject Test in Chinese with Listening Test Prep
- MBLEX - Massage & Bodywork Licensing Examination Courses & Classes
- SE Exam - Professional Licensed Engineer Structural Engineering Exam Courses & Classes
- Connecticut Bar Exam Courses & Classes
- FRM Test Prep
- SAT Subject Test in Chinese with Listening Courses & Classes
- Criminal Psychology Tutors
- Engraving Tutors
- Mississippi Bar Exam Test Prep
- GIAC - Global Information Assurance Certification Courses & Classes