One-to-One Functions
A function is -to- if no two elements in the domain of correspond to the same element in the range of . In other words, each in the domain has exactly one image in the range. And, no in the range is the image of more than one in the domain.
If the graph of a function is known, it is easy to determine if the function is -to- . Use the Horizontal Line Test. If no horizontal line intersects the graph of the function in more than one point, then the function is -to- .
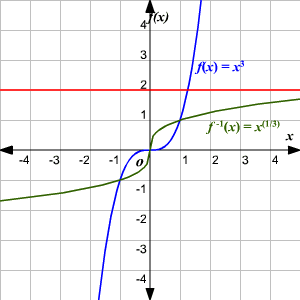
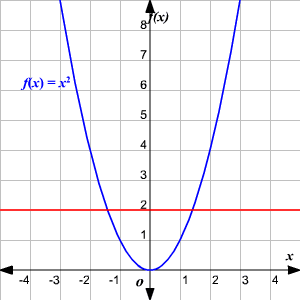
A function has an inverse (read inverse) if and only if the function is -to- .
Properties of a -to- Function:
1) The domain of equals the range of –1 and the range of equals the domain of .
2) for every in the domain of and for every in the domain of –1 .
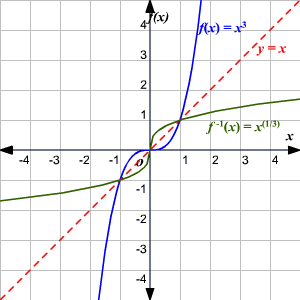
3) The graph of a function and the graph of its inverse are symmetric with respect to the line .
- UK A Level Politics Tutors
- SAT Reading Test Prep
- TEFL - Teaching English as a Foreign Language Training
- LSAT Test Prep
- ISEE Tutors
- Actuarial Exam IFM Test Prep
- CompTIA Test Prep
- CCNA Cloud - Cisco Certified Network Associate-Cloud Test Prep
- Nevada Bar Exam Courses & Classes
- AWS Certified SysOps Administrator Tutors
- Series 27 Test Prep
- Oklahoma Bar Exam Courses & Classes
- Accelerated Algebra Tutors
- CISM - Certified Information Security Manager Courses & Classes
- NBDE Courses & Classes
- OIT Exam Tutors
- SolidWorks Training
- CCNA Routing and Switching - Cisco Certified Network Associate-Routing and Switching Test Prep
- ABIM Exam - American Board of Internal Medicine Courses & Classes
- ISEE Tutors