irrationals
An irrational number is any real number that cannot be expressed in the form a/b when a and b are both integers and b does not equal 0. Put another way, an irrational number is any real number that cannot be expressed as a ratio of integers. In decimal form, irrational numbers never terminate (or end) or fall into a repeating pattern. The digits just go on forever in a nonrepeating manner.
The ancient Greeks were the first to discover that not all numbers are rational; some equations cannot be solved using ratios of integers. The first such question to be studied regarded a square with side lengths one, what is the distance across its diagonal? In algebraic form (which came much later than the Greeks) this is equivalent to . What number times itself equals 2?
The answer is , which is equivalent to approximately 1.414. works out to 1.999396, a number that's very close to 2 but slightly lower. Increasing the number to 1.415 and squaring it gives you 2.002225, meaning we've gone slightly over. You'll never get the exact number 2 by squaring a fraction or terminating decimals. That means that the square root of 2 is an irrational number, a decimal that goes on forever without any repeating pattern. Furthermore, the square root of any real number that isn't a perfect square is an irrational number.
According to legend, the ancient Greek mathematician who proved that could not be written in format angered his colleagues so much that they threw him off of a boat to drown. Other accounts are a little more favorable, saying that the mathematician was merely exiled for turning mathematics on its head rather than executed. Either way, many more irrational numbers have since been discovered. Throwing your friends off of a boat will not help you understand irrationals, but this article might!
Examples of irrationals
You're probably already familiar with at least one irrational number if you've studied the geometry of a circle. The number 3.14 is frequently substituted for the value of pi (expressed with a symbol), but it's only an approximation. The actual decimal goes on forever with no repeating pattern, looking something like this:
3.14159265358979…
Can you imagine having to work with all of those numbers every time you tried to calculate the circumference of a circle? Your teachers can't either, which is why it's acceptable to substitute 3.14 or leave your answers in terms of pi.
Another common irrational number is the golden ratio, a number very important to the study of biology. The golden ratio can be expressed like this:
The most important number in calculus is e, yet another irrational number. It's equivalent to approximately:
It is sometimes more beneficial to think in terms of groups of irrational numbers instead of specific examples. We noted above that all square roots are irrational save for perfect squares, and the same is true for cubic roots, fourth roots, and all other roots outside of a few "perfect" examples. Similarly, many logarithms are among the easiest irrational numbers to prove.
If you consider the real number system as a whole, it contains an uncountable number of numbers. However, rational numbers are both infinite and less dense than their irrational counterparts. Therefore, the vast majority of real numbers are irrational even if most of the numbers we work with every day are rational. Learning about irrationals is like a gateway to the true power of mathematics!
Classification of irrationals
Irrational numbers can be further subdivided into two categories:
- Algebraic numbers that are the solution to some polynomial equation (such as 2 and the golden ratio)
- Transcendental numbers that are not solutions to a polynomial equation (like pi and e)
Keeping track of all of these different types of numbers can be challenging, so here's a Venn diagram to help you remember what is what:
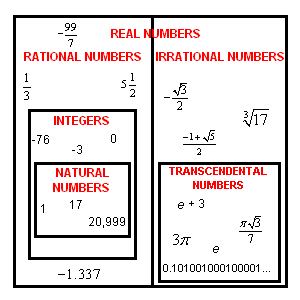
Everything on the right side is an irrational number, but transcendental numbers are in their own box separate from the rest of the irrationals. You should also note that everything in the box above qualifies as a real number including the irrationals, but the rational numbers are clearly separated from the irrationals.
Practice questions on irrationals
a. Is the fraction an irrational number? Why or why not?
No, there is a clear pattern when written in decimal form
b. Is an irrational number? Why or why not?
No, 2 can be expressed in form as
c. Is an irrational number? Why or why not?
Yes, there is no repeating pattern or end to the decimal form.
d. Write an example of a transcendental irrational number:
e. Write an example of an algebraic irrational number:
Any square root beside a perfect square, the golden ratio
Topics related to the irrationals
Flashcards covering the irrationals
Practice tests covering the irrationals
College Algebra Diagnostic Tests
Varsity Tutors can assist with irrationals today
It can be difficult for students to think about decimals with an infinite number of digits, but a good grasp of irrational numbers is essential for success in geometry, calculus, and even the sciences. If your student is struggling now, take action before any current problems spiral out of control. A 1-on-1 math tutor can patiently explain what irrationals are and how they work until it clicks for the student in your life. The Educational Directors at Varsity Tutors would be happy to answer any questions you might have and get your student started today.
- CISSP - Certified Information Systems Security Professional Courses & Classes
- EMT Certification Courses & Classes
- HSPT Verbal Tutors
- Ohio Bar Exam Courses & Classes
- Cisco Training
- CLEP French Test Prep
- Mineralogy Tutors
- CAHSEE Mathematics Tutors
- Southeast Asian Studies Tutors
- SHSAT Courses & Classes
- Tennessee Bar Exam Courses & Classes
- CogAT Courses & Classes
- AP Japanese Language and Culture Tutors
- Series 52 Test Prep
- Six Sigma Training
- MCSD - Microsoft Certified Solutions Developer Test Prep
- Spanish Lessons
- New Mexico Bar Exam Test Prep
- Pre-Calculus for Business Tutors
- Malacology Tutors