Adding Fractions
When adding fractions, the first thing to check is if the denominators are the same.
Adding Fractions with Like Denominators
Fractions with the same denominators are called like fractions.
To add fractions with like denominators, add the numerators , and write the sum over the denominator.

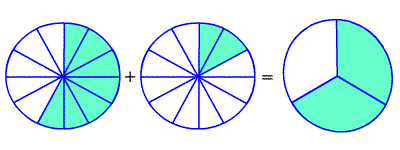
Example :
Find .
Since the denominators are the same, add the numerators.
You may get an answer which is not in lowest terms , even if the fractions you were adding and subtracting both were. In this case, you have to reduce the fraction .
Adding Fractions with Unlike Denominators
If the denominators are not the same, then you have to use equivalent fractions which do have a common denominator . To do this, you need to find the least common multiple (LCM) of the two denominators.
For example, suppose you want to add:

The LCM of and is . So, we need to find fractions equivalent to and which have in the denominator. Multiply the numerator and denominator of by , and multiply the numerator and denominator of by .
Now we have like denominators, and we can add as described above.

- Florida Bar Exam Test Prep
- OAT Courses & Classes
- Series 26 Test Prep
- SAT Subject Test in Biology E/M Test Prep
- SAT Subject Test in United States History Courses & Classes
- CIA - Certified Internal Auditor Courses & Classes
- MCSD - Microsoft Certified Solutions Developer Test Prep
- CLEP French Courses & Classes
- Medicinal Chemistry Tutors
- Certified ScrumMaster Courses & Classes
- ARDMS - American Registry for Diagnostic Medical Sonography Courses & Classes
- SAT Writing and Language Courses & Classes
- Certified Ethical Hacker Test Prep
- 10th Grade Reading Tutors
- Pedology Tutors
- Microsoft Training
- German Courses & Classes
- OAT Courses & Classes
- Delaware Bar Exam Test Prep
- Series 66 Test Prep