Sine Function
You've probably studied a variety of functions by now, one of the most important in trigonometry as the sine function. The sine function is a periodic function, meaning that its graph behaves cyclically by repeating itself over and over from left to right. The graph of is below for reference:
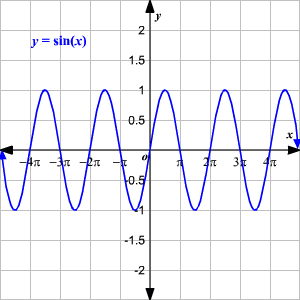
If that doesn't make much sense, don't worry about it. This article will look at the sine function in other ways to make it a more useful tool in your mathematics repertoire. Let's get started!
Understanding the sine function
The easiest way to examine the sine function is to use the unit circle. For any given angle measure θ, we can draw a unit circle on the coordinate plane with the angle centered at the origin and the positive x-axis as one side. This is what it should look like:
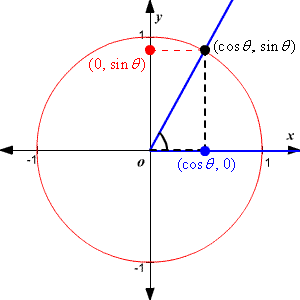
The y-coordinate of the point on the circle is , and the x-coordinate is .
Using the sine function to memorize important values
While we don't need to use the sine function to illustrate important sine values, having a visual can only help. The following diagram highlights the properties of 45-45-90 right triangles using the sine function:
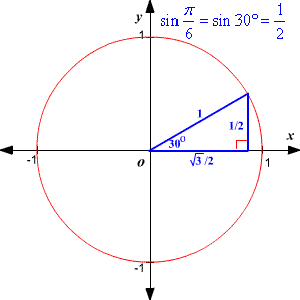
If you haven't memorized this information yet, seeing it like this may help you. Similarly, the diagrams below illustrate important sine values for 30-60-90 right triangles:

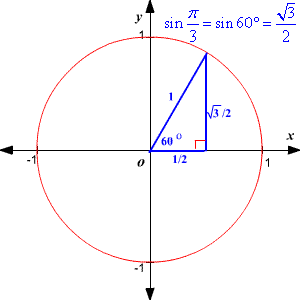
The true value of the sine function is revealed when we start using the values above to calculate other values. The diagram below provides a lot of information in a relatively small space:
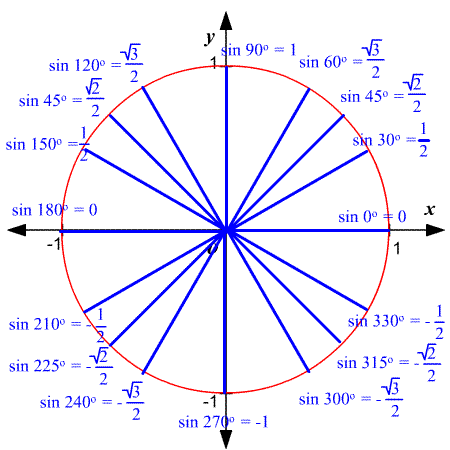
Remember that the value of sin(θ) will be positive in quadrants I and II and negative in quadrants III and IV.
Deepening our understanding of the sine function
The period of is , meaning that it starts repeating at every interval of . Therefore, we can see the whole graph by sketching it on the coordinate plane with x values from 0 to :
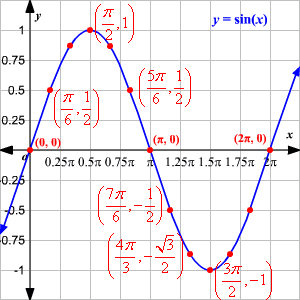
If we extended the x-axis beyond , the curve would repeat the pattern above. Therefore, the image above is the "standard" depiction of the sine function when graphed as a line. Put another way, the domain of the sine function is all real numbers while the range is .
Unlike parabolas, the sine function doesn't have a vertex with a clear highest or lowest point. Since the highest and lowest points repeat every ` ` tough, we can express both algebraically:
Highest point: , where n must be an integer
Lowest point: , where n must be an integer
Modifying the sine function
While the rules above are true for the basic sine function , things change slightly if we're working with more complex functions. The standard form of a sine function is:
We use the a value to determine the amplitude of the function, or how far it goes above and below the x-axis. The amplitude doesn't change the x-intercepts of the graph, just what the y values are. The diagram below illustrates this by comparing the graph of f :
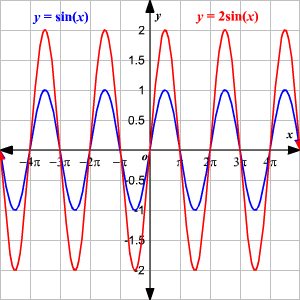
The domain of the red graph above is still all real numbers, but the range has increased to . Importantly, it doesn't matter if a is positive or negative. The absolute value of 'a' ( ) determines the amplitude. Put another way, and have the same amplitude.
Likewise, the 'b' value affects the period of the sine function, or how long it takes to repeat. The formula is:
The 'b' value of and is 1, which means that both functions have the same period. If we substitute 1 into the formula above, we get:
That works out to , which is the period of the standard sine function. Note that we're using absolute value again, so 'b' can be positive or negative without changing the period.
Practice questions on sine function
a. Find the amplitude of the following sine function:
The amplitude is the absolute value of a when the function is written in standard form. The absolute value of this function is 3, making 3 our amplitude.
b. Define the domain and range of the following sine function:
The amplitude of a sine function determines its range, so we need to start with that. The a value is 4 and the absolute value of 4 is still 4, so we have our amplitude. That means that the range of this function is . The domain is x can be all real numbers for any sine function.
c. Find the period of the following sine function:
The formula for determining the period of a sine function is . Our b value is -4, so we take the absolute value of that and put it under the . That gives us:
That works out to , meaning that the pattern repeats every .
d. Find the amplitude and period of the following sine function:
This problem gives us a and b values to work with. Let's begin with the amplitude. The a value is -3, so we take the absolute value of that for an amplitude of 3.
Next, we take the absolute value of b (2) and plug it into our period formula:
That works out to . Therefore, we've successfully solved the problem. The amplitude is 3, and the period is .
Topics related to the Sine Function
Amplitude and Period of Sine and Cosine Functions
Amplitude and Period of Sine and Cosine Functions
Flashcards covering the Sine Function
Practice tests covering the Sine Function
Trust Varsity Tutors to deepen your understanding of the sine function and its properties
Working with sine functions demands a blend of trigonometry and graphing, and many students struggle with it. If you could use a helping hand to reach for your educational potential, a 1-on-1 math tutor can provide personalized support such as customized lesson plans. Your academic mentor can also help you create a distraction-free learning environment to help you focus on mathematics. If you would like to learn more about the potential benefits of tutoring or are ready to get started, the Educational Directors at Varsity Tutors would love to hear from you.
- Alaska Bar Exam Courses & Classes
- French Lessons
- CGEIT - Certified in the Governance of Enterprise IT Test Prep
- Series 23 Test Prep
- Ecology Tutors
- Michigan Bar Exam Courses & Classes
- CCA-N - Citrix Certified Associate - Networking Courses & Classes
- Odia Tutors
- Series 53 Test Prep
- CLEP Introduction to Business Law Tutors
- Bilingual Education Tutors
- US Constitutional History Tutors
- WEST-E Tutors
- Institutional Economics Tutors
- Advanced Functions Tutors
- Computer Game Design Tutors
- CBEST - The California Basic Educational Skills Test Courses & Classes
- Wisconsin Bar Exam Test Prep
- AFOQT - Air Force Officer Qualifying Test Test Prep
- Series 31 Courses & Classes