Absolute Value Inequalities
You know what absolute value is and you've worked with inequalities before. But did you know that both of these concepts can be combined with algebra?
An absolute value inequality is defined as an inequality that has an absolute value sign with a variable inside. In this article, we'll explore what these inequalities mean, how to solve them, and how to graph them. Let's get started!
Absolute value inequalities with a < symbol
The inequality means that the distance between x and 0 is less than 4. Here is what it looks like once graphed:
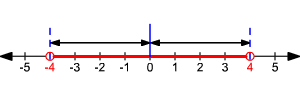
This means that and , allowing us to write the following solution set: .
Inequalities like this always give us two cases to consider. First, the expression inside the absolute value symbol could be positive. Alternatively, the expression could be negative. We have to account for both cases in our answer, so the solution is the intersection between them.
In general terms, for any real numbers a and b, if , then and .
This might become easier to understand with a little practice, so let's work on a sample problem. Let's solve and graph .
Solving this type of inequality requires us to convert it into a compound inequality, so let's start with that:
and
Next, we isolate the variable by adding 7 to both expressions:
That gives us:
Finally, we can graph our answer:

Note that the inequality signs we're using preclude the possibility of x being equal to 4 or 10, so the line above doesn't include them. Coloring in those circles is an easy mistake to make, so we have to be proactive about avoiding it.
Absolute value inequalities with a > symbol
The inequality means that the distance between x and 0 is greater than 4 units. Here is what it looks like once graphed:
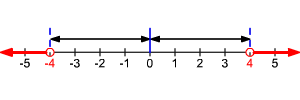
In this case, or . We can write the resulting solution set as . Once again, there are two cases to consider: one where the expression inside the absolute value symbol is positive and another where it's negative. For any real numbers a and b, if , then and .
Let's put this into practice by solving and graphing the following inequality:
First, we need to split this into two separate inequalities:
or
Next, we isolate the variable in each inequality by subtracting 2 from each side:
or
Now that we have our solution set, we can create the following graph:
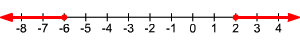
Note that the circles are filled in this time because our inequality used a "≥" symbol, not a ">" symbol. Paying attention to the symbols you're using is essential when working with inequalities.
Practice questions on absolute value inequalities
a. Solve for x:
We can simplify this inequality by subtracting 7 from each side, so let's start with that:
After that, we need to split the inequality into two separate ones since we're working with absolute value. The two inequalities will be:
and
Be careful with the inequality symbols during this step! The second sign must be the reverse of the one we started with to account for the effect of absolute value on negative numbers. Naturally, solving two different inequalities will give us two different solutions:
or
Both of these inequalities must be fulfilled for the original statement to be true, so our solution set is:
b. Solve for x:
For inequalities like this, we can solve for positive values by ignoring the absolute value sign entirely and negative values by switching the inequality symbol and adding a negative sign to the 7. So, the positive value will be:
The negative value will be:
Our final answer is ,
c. Solve for x:
This is actually a trick question. The absolute value of a real number is always greater than zero, so there's no potential value of x where . Therefore, the correct answer to this question is no solution.
Topics related to the Absolute Value Inequalities
Flashcards covering the Absolute Value Inequalities
Practice tests covering the Absolute Value Inequalities
College Algebra Diagnostic Tests
Trust Varsity Tutors to deepen your student's understanding of absolute value inequalities
Many students haven't thought about absolute value or inequalities for a while by the time they begin studying absolute value inequalities, leading some to confusion and even panic. If you or your student could benefit from a helping hand, an experienced academic mentor could guide you through practice problems step-by-step until you're comfortable moving on to a fresh topic. A private tutor can also help you set up a distraction-free study space to make it easier to concentrate on your work. Reach out to the Educational Directors at Varsity Tutors today to learn more.
- API - Associate in Personal Insurance Test Prep
- CSRM - Certified School Risk Manager Courses & Classes
- CLEP College Algebra Test Prep
- OAE - Ohio Assessments for Educators Tutors
- Kansas Bar Exam Test Prep
- Legal Research Tutors
- Radical Functions Tutors
- C2 Courses & Classes
- NBDE Courses & Classes
- French Courses & Classes
- Personality Psychology Tutors
- Series 22 Test Prep
- CIMA Test Prep
- TSI - Texas Success Initiative Assessment Tutors
- Series 10 Test Prep
- CRM - Certified Risk Manager Courses & Classes
- MOS - Microsoft Office Specialist Courses & Classes
- CLEP Western Civilization I: Ancient Near East to 1648 Courses & Classes
- VTNE - Veterinary Technician National Exam Courses & Classes
- Quantitative Analysis Tutors