Hyperbolas
The "basic" hyperbola is the function
This function has a graph which consists of two disjoint parts. Note that is not in the domain . Note also that the function approaches asymptotically as grows infinitely large (or infinitely negative), and that it approaches infinity as approaches from the positive side, negative infinity as approaches from the negative side.
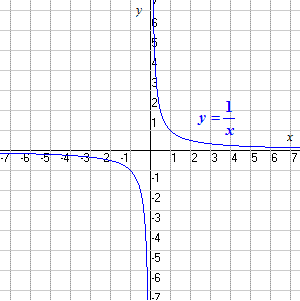
The center of the hyperbola is the point of rotational symmetry. In the above example, the center is .
The graph of the rational function
is a hyperbola whose center is . The constant controls the "steepness" with which the graph approaches the asymptotes .
A hyperbola can also be defined as a conic section obtained by the intersection of a double cone with a plane that is intersects both pieces of the cone without intersecting the axis.

- BCABA - Board Certified Assistant Behavior Analyst Test Prep
- Math Test Preparation Tutors
- Series 57 Test Prep
- Type Design Tutors
- CIMA Courses & Classes
- SAT Subject Test in Japanese with Listening Test Prep
- VTNE - Veterinary Technician National Exam Courses & Classes
- C2 Courses & Classes
- REGENTS Tutors
- Series 9 Courses & Classes
- SHSAT Courses & Classes
- ISEE-Upper Level Reading Comprehension Tutors
- Banjo Tutors
- CTRS - A Certified Therapeutic Recreation Specialist Test Prep
- High School Math Tutors
- PHR - Professional in Human Resources Test Prep
- Virginia Bar Exam Test Prep
- New Hampshire Bar Exam Courses & Classes
- New York Bar Exam Courses & Classes
- Ohio Bar Exam Test Prep