Describing the Graph of a Function
Sometimes you need to describe the graph of a function in a non-symbolic way. For example, you may be asked
- whether a function is increasing or decreasing;
- whether it has one minimum value or maximum value, or several such values
- whether it is linear or not
- whether the rate of change is constant, increasing, or decreasing
- whether it has an upper or lower bound.
Example 1:
Describe the two functions and , using the terms increasing, decreasing, maxima and minima.
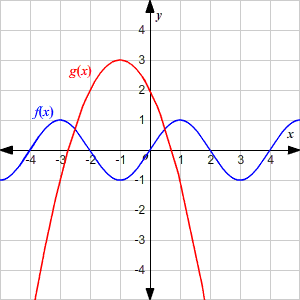
It has a maximum value of and a minimum value of , and it attains these maxima and minima many times. The upper bound of the function is and the lower bound is .
The graph of is increasing for and decreasing for . The graph takes a maximum value of at . It has no minimum.
Example 2:
Which graph has a greater rate of change?

Both graphs start together at . At first, the linear function, , has the faster rate of change.
But soon catches up, and surpasses at , and continues increasing at a faster rate.
- MCSD - Microsoft Certified Solutions Developer Courses & Classes
- IB Geography SL Tutors
- Certified ScrumMaster Test Prep
- Arizona Bar Exam Courses & Classes
- ACT Math Courses & Classes
- American Politics Tutors
- Chemistry REGENTS Tutors
- Russian Courses & Classes
- PCAT Verbal Ability Tutors
- New York Bar Exam Courses & Classes
- REGENTS Tutors
- CTRS - A Certified Therapeutic Recreation Specialist Courses & Classes
- CLEP Financial Accounting Tutors
- ARM-P - Associate in Risk Management for Public Entities Test Prep
- Spanish 3 Tutors
- Colorado Bar Exam Courses & Classes
- Stoichiometry Tutors
- IB Language A: Language and Literature Tutors
- Utah Bar Exam Courses & Classes
- IB Sports, Exercise and Health Science SL Tutors