Comparing Linear, Polynomial, and Exponential Growth
One of the most interesting things about algebra is that different kinds of equations take different shapes when we graph them on a plane. But what exactly is the difference between linear, polynomial, and exponential growth when we graph these functions? Let's find out:
Putting all three functions on a plane
Consider these three functions:
What do these functions look like when we graph them? Let's take a look:
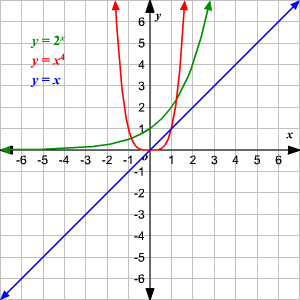
The interesting thing about graphing functions is that their shape represents their type. For example, the blue function is linear, so it takes the shape of a straight line. The red function is polynomial, so it takes the form of a parabola. The green function is exponential, so it takes the shape of an upward curve.
Making our comparisons
Once we understand how the functions work, it's easier to compare them. For example, what if we wanted to find the function that grows the fastest if we increase the value of x? Take a look:
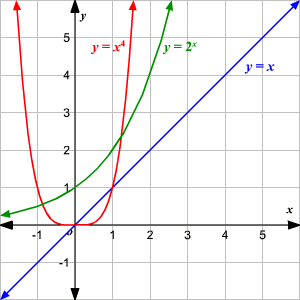
At first glance, it might seem like the parabola is the clear winner. But what happens when we zoom out? Take a look:
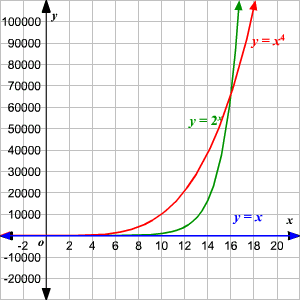
As we can see, the equation for exponential growth overtakes the parabola at . This teaches us a useful lesson: At some point, the exponential function with base greater than 1 will always outstrip the polynomial function.
Topics related to the Comparing Linear, Polynomial, and Exponential Growth
Graphing Exponential and Logarithmic Functions
Flashcards covering the Comparing Linear, Polynomial, and Exponential Growth
Practice tests covering the Comparing Linear, Polynomial, and Exponential Growth
College Algebra Diagnostic Tests
Pair your student with a suitable tutor who understands how to compare linear, polynomial, and exponential growth
If your student needs help comparing polynomial, exponential, and linear growth, 1-on-1 tutoring is a clear option. During tutoring sessions, your student's tutor can choose the appropriate pace -- whether they want to steam ahead or slow down to hammer down key concepts. Tutors can also personalize the lesson plan by catering to your student's learning style, hobbies, and much more. Speak with our Educational Consultants today and rest assured: Varsity Tutors will pair your student with a suitable tutor.
- Catalan Tutors
- CRISC - Certified in Risk and Information Systems Control Training
- AFOQT - Air Force Officer Qualifying Test Test Prep
- CRISC - Certified in Risk and Information Systems Control Courses & Classes
- PE Exam - Professional Licensed Engineer Principles and Practice of Engineering Exam Courses & Classes
- 12th Grade Math Tutors
- Delaware Bar Exam Test Prep
- CLEP Principles of Microeconomics Courses & Classes
- Old Norse Tutors
- World Studies Tutors
- Kindergarten Homework Tutors
- IB Further Mathematics Tutors
- Oology Tutors
- 8th Grade Tutors
- CCENT - Cisco Certified Entry Networking Technician Courses & Classes
- ACSM - American College of Sports Medicine Courses & Classes
- Abkhaz Tutors
- AP US History Tutors
- Conceptual Math Tutors
- CPPA - Certified Professional Public Adjuster Courses & Classes