Cramer's Rule
Gabriel Cramer lived in the 18th century, and he made various contributions to the field of math. One of his most enduring contributions was Cramer's Rule -- a formula that helps us solve certain systems of linear equations. But how exactly does this rule work? When and how should we use it to solve our own systems of linear equations? Let's find out:
What is Cramer's Rule?
Before we get into Cramer's Rule, we need to review the concept of a "determinant."
We may recall that when we see a system of linear equations, there are only three possibilities:
- The lines intersect at a unique point (only one solution).
- The lines occupy the same position (infinite solutions).
- The lines are parallel (no possible solutions).
We can determine whether we have a unique solution (only one intersecting point) relatively easily. If the linear functions are equivalent, they must occupy the same space (infinite solutions). If the lines have the same slope, they must be parallel (no possible solutions). If none of these characteristics apply to our system of linear equations, we know that we must have a unique solution.
Consider the following system of linear equations:
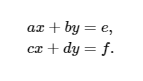
We can write this as a matrix:
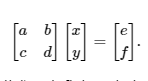
Note that if , then the system has only one intersecting point. If , then the system either has zero solutions (parallel) or infinite solutions (equivalent equations). In other words, this value helps us determine what type of solution we can expect for our system of linear equations. This is why it is called the determinant. We can write this determinant in a number of different ways, including:
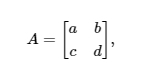
and express the determinant as or .
Note the pattern here: When finding the determinant of a matrix, we need to find the difference of the diagonal values in the matrix. For example, the determinant of this:
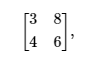
is calculated as:
But why are determinants relevant to Cramer's Rule?
Well, Cramer's Rule involves using determinants to solve systems of linear equations.
Consider the following system of linear equations:
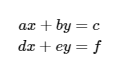
We know that if , then:
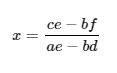
And:
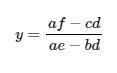
We note that the denominators of these expressions are equal to the determinant of the coefficients matrix:
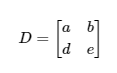
Not only that, but the numerators are also equal to the determinants and :
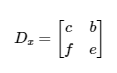
And:
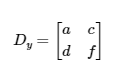
Here, for , we replaced the column of coefficients of in with the column of constants from the system of equations. For , we replaced the column of coefficients of in with the column of constants.
In other words, we are replacing the column for a particular variable with the "answer" column. This answer column represents the values that come after the "equals" sign in our system of equations.
You might have noticed that by using Cramer's rule, we could potentially solve for just one variable in a system of equations without having to solve the entire system first. This is useful if we only need one variable -- especially if we're dealing with many equations in many unknowns.
This is best illustrated with the following expressions:
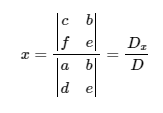
And:
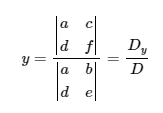
Those last terms are the most important:
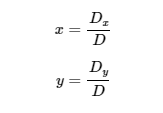
We can also continue to expand this if our system has more variables and equations. For example, we could add:
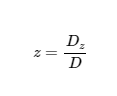
In other words, Cramer's Rule can help us use determinants to solve a system of linear equations in three variables!
Putting Cramer's Rule into action
Let's try to use Cramer's Rule to solve a system of linear equations:
We begin by identifying the coefficients in the system of linear equations:
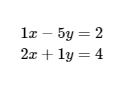
This corresponds to:
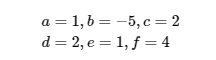
We can calculate the determinant D of the coefficient matrix as follows:
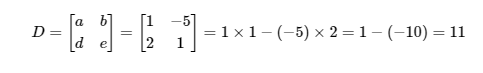
Now let's calculate the determinants and :
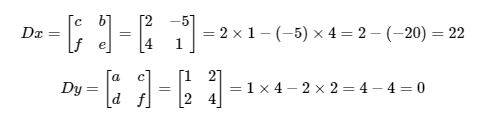
Now we apply Cramer's Rule:
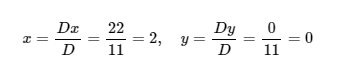
Great! Now we know that our solution must be . . Hopefully, we now understand how Cramer's Rule makes it easy to solve linear equations that might otherwise be a little tricky. It's a great tool to have under our belts as we progress into more advanced mathematics.
A short history of Cramer's Rule
Cramer's Rule is named after none other than Gabriel Cramer -- a Genevan mathematician who lived in the early to mid-18th century. He received his doctorate in mathematics at age 18 at the University of Geneva. During his 20s, he proposed a solution to the St. Petersburg Paradox, contributing to the development of expected utility theory. During his 40s, he made significant contributions to the field of algebraic curves. Two years before his passing in 1752, he published Cramer's Rule. Even after almost 300 years, this rule is still considered standard. However, there is some debate as to whether Cramer was the first to conceptualize the rule. Colin Maclaurin published special cases of the rule in 1748, and some believe that this Scottish mathematician was aware of the rule almost 20 years prior.
Topics related to the Cramer's Rule
Writing Systems of Linear Equations from Word Problems
Flashcards covering the Cramer's Rule
Practice tests covering the Cramer's Rule
Pair your student with a suitable math tutor who understands Cramer's Rule
Cramer's Rule might be challenging to understand, but it can be very useful throughout the rest of your student's mathematical journey. This is why it makes sense to have your student work with an experienced tutor who can explain Cramer's Rule -- and many other concepts -- in an encouraging, personalized 1-on-1 environment. If your student doesn't quite understand one aspect of Cramer's Rule, their tutor can slow things down to a more manageable pace. Once your student fully understands the concept at hand, they can let their tutor know that they're ready to move on. This is only one example of tutoring's personalized features that are difficult to replicate in a classroom setting. Speak with our Educational Directors today to learn more, and rest assured: Varsity Tutors will match your student with an appropriate tutor.
- GRE Subject Test in Chemistry Test Prep
- Algebra 3/4 Tutors
- Human Resources Tutors
- AP Statistics Tutors
- Utah Bar Exam Courses & Classes
- AICE Math Tutors
- Basque Tutors
- CPFA Courses & Classes
- Series 3 Test Prep
- Quickbooks Training
- 9th Grade English Tutors
- AWS Certified Solutions Architect Courses & Classes
- Michigan Bar Exam Courses & Classes
- Business Administration Tutors
- CMT - Chartered Market Technician Courses & Classes
- Foreign Languages Tutors
- MLT Exam Test Prep
- Georgia Bar Exam Courses & Classes
- WISC V Test Prep
- Series 32 Courses & Classes