Cono
Un cono es un solido compuesto de un círculo y su interior ( base ), un punto dado no en el plano del círculo ( vértice ) y todos los segmentos del punto al círculo.

El radio del cono es el radio de la base. La altitud del cono es el segmento perpendicular del vértice al plano de la base. La altura del cono es la longitud de la altitud.
El eje del cono es el segmento cuyos puntos finales son el vértice y el centro de la base. Si el eje es perpendicular al plano del círculo, el cono es un cono recto , de otro modo es un cono oblicuo .
La altura de inclinación de un cono recto es la longitud del segmento del vértice del cono al círculo de la base. La altura de inclinación no está definida para los conos oblicuos.
Un cono está cercanamente relacionado a una pirámide . Así, las fórmulas para sus áreas de superficie y volumen están relacionadas.

Recuerde, las fórmulas para el
área de superficie
lateral
de una pirámide
es
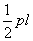 y el área de superficie total es
y el área de superficie total es
 .
.
Ya que la base de un cono es un círculo, sustituimos 2 π r por p y πr 2 por B donde r es el radio de la base del cono.
Así, la fórmula para el área de superficie lateral de un cono recto es L. S. A. = πrl , donde l es la altura de inclinación del cono .
Ejemplo 1:
Encuentre el área de superficie lateral de un cono recto si el radio es de 4 cm y la altura de inclinación es de 5 cm.

L. S. A. = π (4)(5) = 20 π ≈ 62.82 cm 2
La fórmula para el área de superficie total de un cono recto es T. S. A. = π rl + π r 2 .
Ejemplo 2:
Encuentre el área de superficie total de un cono recto si el radio es de 6 pulgadas y la altura de inclinación es de 10 pulgadas.

T. S. A. = π (6)(10) + π (6) 2
= 60 π + 36 π
= 96 π inches 2
≈ 301.59 inches 2
Ya que la altura de inclinación es indefinida para un cono oblicuo, no hay fórmulas para las áreas de conos oblicuos.
El
volumen
de un cono circular es un tercio del producto de su altitud y el área de su base.
 .
.
Ejemplo 3:
Encuentre el volumen de un cono cuya altitud es de 15m y cuyo radio es de 8m.


≈ 1005.31m 2
- CCP-V - Citrix Certified Professional - Virtualization Courses & Classes
- CLEP English Literature Test Prep
- MTC - Missouri Teacher Certification Courses & Classes
- Tom Clancy's Rainbow Six Siege Tutors
- Series 24 Courses & Classes
- Research Writing Tutors
- BCABA - Board Certified Assistant Behavior Analyst Courses & Classes
- CPFA Courses & Classes
- CMT - Chartered Market Technician Courses & Classes
- Washington Bar Exam Test Prep
- GRE Subject Test in Biology Test Prep
- Web Development Tutors
- Chemistry Tutors
- MCSE - Microsoft Certified Solutions Expert Test Prep
- CLEP History of the United States II: 1865 to the Present Tutors
- Series 66 Courses & Classes
- Orthography Tutors
- Alabama Bar Exam Courses & Classes
- AWS Certification - Amazon Web Services Certification Courses & Classes
- Alaska Bar Exam Test Prep