Transformations
There are three kinds of isometric transformations of -dimensional shapes: translations, rotations, and reflections. ( Isometric means that the transformation doesn't change the size or shape of the figure.) A fourth type of transformation, a dilation , is not isometric: it preserves the shape of the figure but not its size.
Translations
A translation is a sliding of a figure. For example, in the figure below, triangle is translated units to the left and units up to get the image triangle .
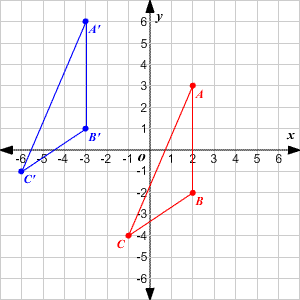
This translation can be described in coordinate notation as .
Rotations
A second type of transformation is the rotation . The figure below shows triangle rotated clockwise about the origin.
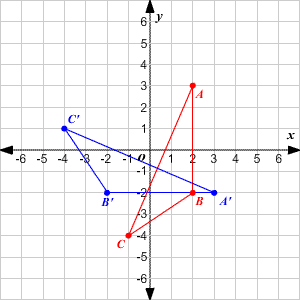
This rotation can be described in coordinate notation as . (You can check that this works by plugging in the coordinates of each vertex.)
Reflections
A third type of transformation is the reflection . The figure below shows triangle reflected across the line .

This reflection can be described in coordinate notation as . (Again, you can check this by plugging in the coordinates of each vertex.)
Dilations
A dilation is a transformation which preserves the shape and orientation of the figure, but changes its size. The scale factor of a dilation is the factor by which each linear measure of the figure (for example, a side length) is multiplied.
The figure below shows a dilation with scale factor , centered at the origin.

This dilation can be described in coordinate notation as . (Again, you can check this by plugging in the coordinates of each vertex.)
- 9th Grade Homework Tutors
- Urban Planning Tutors
- Washington Bar Exam Test Prep
- IB Information Technology in a Global Society HL Tutors
- CGEIT - Certified in the Governance of Enterprise IT Tutors
- CLEP College Composition Test Prep
- Learning Disability Tutors
- Honors Geometry Tutors
- Drama Tutors
- Washington Bar Exam Courses & Classes
- Scottish Gaelic Tutors
- Series 10 Test Prep
- Alabama Bar Exam Test Prep
- Biblical Studies Tutors
- UK A Level Geography Tutors
- Arkansas Bar Exam Test Prep
- COMLEX Courses & Classes
- COMLEX Courses & Classes
- AP Japanese Language and Culture Tutors
- AWS Certified Solutions Architect Courses & Classes