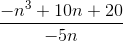All GRE Math Resources
Example Questions
Example Question #281 : Gre Quantitative Reasoning
Choose the answer which best simplifies the following expression:
To simplify this expression, first multiply both terms by the denominator of the other over itself:
Now that you have a common denominator, you may subtract:
Example Question #291 : Algebra
Choose the answer which best simplifies the following expression:
To simplify this problem, multiply each term by the denominator of the other over itself:
Now that both terms share a denominator, you can subtract:
Example Question #11 : Rational Expressions
Choose the answer which best simplifies the following expression:
To solve this problem, first multiply each term of the original expression by the denomenator of the other over itself:
Then you will have two terms with a common denomenator:
Combine the terms and simplify for your final answer:
Example Question #12 : Rational Expressions
Choose the answer which best simplifies the expression below:
To simplify this problem, multiply each term by the denomenator of the other over itself:
Then you will yield terms with a like denomenator, which can be combined:
Example Question #13 : Rational Expressions
Choose the answer which best simplifies the expression below:
To simplify the expression, first multiply each term by the denomenator of the other over itself:
Then you yield terms with common denomenators, which can be combined:
Example Question #14 : Rational Expressions
Choose the answer which best simplifies the following expression:
To simplify, first multiply each of the terms by the denomenator of the other over itself:
Then you will get terms with a common denomenator, which can be combined:
Example Question #1 : How To Subtract Rational Expressions With Different Denominators
Choose the answer which best simplifies the expression below:
To simplify, first multiply each of the terms by the denomenator of the other over itself:
You will yield terms with a common denomenator, which can be combined:
Example Question #291 : Gre Quantitative Reasoning
Choose the answer which best simplifies the expression below:
To simplify, multiply each of the terms by the denomenator of the other, over itself:
You will yield terms with a common denomenator, which can be combined:
All GRE Math Resources