How to find the surface area of a cube
Help Questions
Geometry › How to find the surface area of a cube
One side of a cube is 
Explanation
To find the surface area of a cube, we find the area of a face by multiplying two of its sides together; then, we multiply by 


We know that for this problem, 
The volume of a cube is 
What is the surface area of the cube?





Explanation
Using the volume given, we take it's cube to find the length of the cube: 
Therefore, the length of the cube is 8 cm.
Knowing the properties of a cube, this implies that the width and height of the cube is also 8 cm.
Since all sides are identical, the formula for the surface area is length times width times the number of sides: 
A cube has a sphere inscribed inside it with a diameter of 4 meters. What is the surface area of the cube?
None of these
Explanation
Since the sphere is inscribed within the cube, its diameter is the same length as an edge of the cube. Since cubes have identical side lengths we find the area of one side and then multiply by the number of sides to find the total surface area.
Area of one side:
Total surface area:
If a side of a cube has a length of 
Explanation
Write the formula to find the surface of a cube, where 
Substitute and solve.
A geometric cube has a volume of 
Explanation
We first need to know the edge length before we can solve for surface area. Since we are provided the volume and all edges are of equal length, we can use the formula for volume to get the length of sides:
Now that we know the length of sides, we can plug this value into our surface area formula:
Find the surface area of a cube with a side length of 
Explanation
Write the formula for the surface area of a cube, substitute the length provided in the question, and simplify.
if the side length of a cube is 
Explanation
The formula for the surface area of a cube is:


We are given the length of one side of the cube in question, so we can substitute that value into the surface area equation and solve:
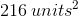




























![\volume=length\cdot width\cdot height\ \27;cm^3=a^3\ \a=\sqrt[3]{27;cm^3}\ \a=3;cm](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/751208/gif.latex)












