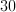How to find an angle in an acute / obtuse triangle
Help Questions
Math › How to find an angle in an acute / obtuse triangle

If the measure of 


Not enough information to solve
Explanation
The key to solving this problem lies in the geometric fact that a triangle possesses a total of 





One could also solve this problem with the knowledge that the sum of the exterior angle of a triangle is equal to the sum of the two interior angles opposite of it.
The largest angle in an obtuse scalene triangle is 

Explanation
Since this is a scalene triangle, all of the interior angles will have different measures. However, it's fundemental to note that in any triangle the sum of the measurements of the three interior angles must equal 
The largest angle is equal to 
Therefore, the final angle must equal:
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
A triangle has sides of lengths 19.5, 46.8, and 50.7. Is the triangle acute, right, or obtuse?
Right
Acute
Obtuse
Explanation
Given the lengths of its three sides, a triangle can be identified as acute, right, or obtuse by the following process:
Calculate the sum of the squares of the lengths of the two shortest sides:
Calculate the square of the length of the longest side:
The two quantities are equal, so by the Converse of the Pythagorean Theorem, the triangle is right.
In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?
Explanation
Since the sum of the angles of a triangle is 

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.

If the measure of 


Not enough information to solve
Explanation
The key to solving this problem lies in the geometric fact that a triangle possesses a total of 





One could also solve this problem with the knowledge that the sum of the exterior angle of a triangle is equal to the sum of the two interior angles opposite of it.
Which of the following can NOT be the angles of a triangle?
45, 45, 90
1, 2, 177
30.5, 40.1, 109.4
45, 90, 100
30, 60, 90
Explanation
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
A triangle has sides of lengths 18.4, 18.4, and 26.0. Is the triangle acute, right, or obtuse?
Acute
Right
Obtuse
Explanation
Given the lengths of its three sides, a triangle can be identified as acute, right, or obtuse by the following process:
Calculate the sum of the squares of the lengths of the two shortest sides:
Calculate the square of the length of the longest side:
The former is greater than the latter. This indicates that the triangle is acute.
In 




A triangle with these sidelengths cannot exist.
Explanation
The sum of the two smallest sides is less than the greatest side:
By the Triangle Inequality, this triangle cannot exist.
A triangle has sides of lengths 14, 18, and 20. Is the triangle acute, right, or obtuse?
Acute
Right
Obtuse
Explanation
Given the lengths of its three sides, a triangle can be identified as acute, right, or obtuse by the following process:
Calculate the sum of the squares of the lengths of the two shortest sides:
Calculate the square of the length of the longest side:
The former is greater than the latter. This indicates that the triangle is acute.