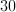Math - Triangles | Practice Hub

What is the hypotenuse of a right triangle with side lengths and ?

Explanation

The Pythagorean Theorem states that . This question gives us the values of and , and asks us to solve for .

Take and and plug them into the equation as and :

$12^{2}+16^{2}=c^{2}$

Now we can start solving for :

$144+256=c^{2}$

$400=c^{2}$

$\sqrt{400}=\sqrt{c^{2}}$

The length of the hypotenuse is .

What is the height of an equilateral triangle with side 6?

$3\sqrt{3}$

$6\sqrt{2}$

Explanation

When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the $60^{\circ}$ ) is $3\sqrt{3}$ .

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?

100

100√2

50√2

200√2

Explanation

Square_part1

Square_part2

Square_part3

Triangle A: A right triangle with sides length , , and .

Triangle B: An equilateral triangle with side lengths .

Which triangle has a greater area?

Triangle B

Triangle A

The areas of the two triangles are the same.

There is not enough information given to determine which triangle has a greater area.

Explanation

The formula for the area of a right triangle is $A = \frac{1}{2}bh$ , where is the length of the triangle's base and is its height. Since the longest side is the hypotenuse, use the two smaller numbers given as sides for the base and height in the equation to calculate the area of Triangle A:

$A = \frac{1}{2}(6)(8)$

The formula for the area of an equilateral triangle is $A = \frac{s^2\sqrt{3}}{4}$ , where is the length of each side. (Alternatively, you can divide the equilateral triangle into two right triangles and find the area of each). Triangle B's area is thus calculated as:

$A = \frac{(8)^2\sqrt{3}}{4}$

$A = \frac{64\sqrt{3}}{4}$

$A = 16\sqrt{3}$

To determine which of the two areas is greater without using a calculator, rewrite the areas of the two triangles with comparable factors. Triangle A's area can be expressed as $24= 8\sqrt{3}\sqrt{3}$ , and Triangle B's area can be expressed as $16\sqrt{3}= (8)(2)\sqrt{3}$ . Since is greater than $\sqrt{3}$ , the product of the factors of Triangle B's area will be greater than the product of the factors of Triangle A's, so Triangle B has the greater area.

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?

100

100√2

50√2

200√2

Explanation

Square_part1

Square_part2

Square_part3

An isoceles triangle has a base angle that is twice the vertex angle. What is the sum of the base and vertex angles?

Explanation

All triangles have degrees. An isoceles triangle has one vertex angle and two congruent base angles.

Let vertex angle and base angle.

So the equation to solve becomes:

Thus for the vertex angle and for the base angle.

The sum of the vertex and one base angle is .

A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?

30m

45m

35m

40m

25m

Explanation

The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.

(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m

What is the hypotenuse of a right triangle with side lengths and ?

Explanation

The Pythagorean Theorem states that . This question gives us the values of and , and asks us to solve for .

Take and and plug them into the equation as and :

$12^{2}+16^{2}=c^{2}$

Now we can start solving for :

$144+256=c^{2}$

$400=c^{2}$

$\sqrt{400}=\sqrt{c^{2}}$

The length of the hypotenuse is .

Exterior_angle

If the measure of $\angle A=52^{\circ}$ and the measure of $\angle B= 43^{\circ}$ then what is the meausre of $\angle\theta$ ?

$95^{\circ}$

$85^{\circ}$

$82^{\circ}$

$98^{\circ}$

Not enough information to solve

Explanation

The key to solving this problem lies in the geometric fact that a triangle possesses a total of $180^{\circ}$ between its interior angles. Therefore, one can calculate the measure of $\angle C$ and then find the measure of its supplementary angle, $\angle\theta$ .

$180^{\circ}=\angle A + \angle B + \angle C$

$\angle C= 180^{\circ}- 52^{\circ} - 43^{\circ}$

$\angle C= 85^{\circ}$

$\angle C$ and $\angle\theta$ are supplementary, meaning they form a line with a measure of $180^{\circ}$ .

$\angle\theta =180^{\circ} - 85^{\circ}$

$\rightarrow 95^{\circ}$

One could also solve this problem with the knowledge that the sum of the exterior angle of a triangle is equal to the sum of the two interior angles opposite of it.

The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?