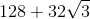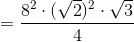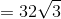Calculating the surface area of a tetrahedron
Help Questions
GMAT Quantitative › Calculating the surface area of a tetrahedron
The slant height of a pyramid is one and one-half times the perimeter of its square base. The base has sides of length 15 inches. What is the surface area of the pyramid?
Explanation
The square base of the pyramid has four sides with length 15 inches, making its perimeter four times that, or 60 inches. The slant height is

Therefore, the area of the base is 
Each of the four lateral triangles has area 
The total surface area is 

Refer to the above diagram, which shows a tetrahedron.


Explanation
Three of the surfaces of the tetrahedron - 




The area of each of these triangles is half the product of its legs, so each area is
Also, the legs are of the same measure among the triangles, the hypotenuses are as well, so the fourth surface 

Add the areas of the faces:
A regular tetrahedron comprises four faces, each of which is an equilateral triangle. If the sum of the lengths of its edges is 120, what is its surface area?
Explanation
As shown in the diagram below, a regular tetrahedron has six congruent edges, so each has length 

The area of one face is the area of an equilateral triangle with sidelength 20, which is
The total surface area is four times this, or 
In three-dimensional space, the four vertices of a tetrahedron - a solid with four faces - have Cartesian coordinates 
Give the surface area of the tetrahedron.
Explanation
The tetrahedron looks like this:



The bottom, front, and left faces are each right triangles whose legs each measure 60. Each face has area

The remaining face has three edges each a hypotenuse of one of three congruent right triangles, so its sides are congruent, and it is an equilateral triangle. Its sidelength can be found via the 45-45-90 Theorem to be 
The total area is
A regular tetrahedron is a solid with four faces, each of which is an equilateral triangle.
If the lengths of all of the edges of a regular tetrahedron are added, the total length is 120. What is the surface area of the tetrahedron?
Explanation
A tetrahedron looks like this:

The tetrahedron has six edges, and in a regular tetrahedron, they are congruent, so each edge has length 
The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula
There are four congruent faces, so the total surface area is
Since 
A regular tetrahedron is a solid with four faces, each of which is an equilateral triangle.
Each edge of a regular tetrahedron has length 
Explanation
The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula
There are four congruent faces, so the total surface area is
Since 

The cube in the above figure has surface area 384. Give the surface area of the tetrahedron with vertices 
Explanation
The surface area formula can be used to find the length of each edge of the cube:
Three faces of the tetrahedron - 
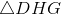


Each triangle is isosceles, so, by the 45-45-90 Theorem, each of their hypotentuses measures 


The total surface area is

Evaluate the surface area of the above tetrahedron.
Explanation
Three of the faces of the tetrahedron are isosceles right triangles with legs of length 8, and, subsequently, by the 45-45-90 Theorem, hypotenuses of length 

Each of the three right triangle faces has area equal to half the product of its legs , which is

The equilateral face has as its area
The sum of the areas of the faces is

The above diagram shows a regular right triangular pyramid. Its base 


Explanation
The base is an equilateral triangle with sidelength 12, so its area can be calculated as follows:

Each of the three other faces is congruent, with base 12. The area of each is the product of its base and its height. To find the common height, we examine 




The area of 
All three lateral faces have this area.
Now add the areas of the four faces: