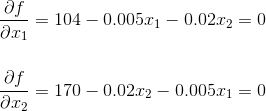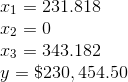All Math Modeling Resources
Example Questions
Example Question #4 : Math Modeling
A cow that weighs 175 pounds gains 3 pounds per day, and it costs 30 cents per day to keep that cow. The market price for cows is 75 cents per pound, but the price is falling one cent per day. When should the cow be sold to make the maximum profit?
Use the 5-step method.
The max profit is $131.58.
The cow should be sold after 2 days.
The max profit is $151.58.
The cow should be sold after 3 days.
The cow should be sold after 4 days.
The cow should be sold after 3 days.
The 5-step method for this particular modeling question is as follows.
1. Ask the question
When should the cow be sold to make the maximum profit?
Now identify all known information.
Variables:
2. Select the modeling approach
For this particular question the function can be define 

3. Formulate the model
To maximize 

Now rewrite the equation in terms of 
4. Solve the model
Now to solve the model, take the derivative, set it equal to zero, and solve for 
5. Answer the question
The cow should be sold after 3 days.
Example Question #5 : Math Modeling
A company that makes computer monitors is unveiling two new products this spring, a 15 inch screen for $189 and a 19 inch screen for $269. The cost to manufacture the 15 inch screens is $85 per screen and the 19 inch screen is $99 per screen, plus $200,000 for miscellaneous costs. The number of sells for each screen type effects the average selling price. It is estimated that each set average selling price drops by two cents for each additional screen sold. The average sells price for the 15 inch screen will decrease by 0.2 cents for each 19 inch screen sold, the price of the 19 inch screen decreases by 0.3 cents for each 15 inch screen sold. What are the partial differential equations used to find how many units of each type of screens should be manufactured to optimize profit?
First, identify all known information.
Variables:
Assumptions:

Objective:
Maximize the profit.
Theorem: If 





Therefore, to find the maximum point in this function, simultaneously solve the differential equations in question and check the boundary points.
Now switch variables/
Over
From here take the partial differential equation of each variable. Since the questioned asked for the partial differential equations that would be used to optimize the profit we can stop here.
Example Question #1 : Math Modeling
Using Newton's Method as the computational method, optimize the follow problem.
A cow that weighs 175 pounds gains 3 pounds per day, and it costs 30 cents per day to keep that cow. The market price for cows is 75 cents per pound, but the price is falling one cent per day. When should the cow be sold to make the maximum profit?
It is recommended to wait 6 or 7 days to sell the cow. This should result in a net profit of $130.
It is recommended to wait 2 or 5 days to sell the cow. This should result in a net profit of $131.90.
It is recommended to wait 8 or 9 days to sell the cow. This should result in a net profit of $132.90.
It is recommended to wait 9 or 10 days to sell the cow. This should result in a net profit of $132.
It is recommended to wait 7 or 8 days to sell the cow. This should result in a net profit of $131.90.
It is recommended to wait 7 or 8 days to sell the cow. This should result in a net profit of $131.90.
Assume that the growth rate of the cow is proportional to its weight.
In mathematical terms:
Looking at the known information,
Variables:
Therefore,

when
Thus the differential equation to solve for 
Solving by separation of variables results in the following equation.
From here, formulate the model with the new weight equation.
Recall that the goal is to optimize the question over

Use a graphing calculator or computer technology to graph the function.

Observing the graph it appears the maximum profit for the cow occurs around 

From here, answer the question. Taking into account the growth rate of the cow is still increasing, it is recommended to wait 7 or 8 days to sell the cow. This should result in a net profit of $131.90.
Example Question #2 : Math Modeling
A farm has 750 acres of land available for planting crops. The possible crops are soy, corn, and oats. There is 1,200 acre-ft of water for irrigation and the crew will be able to work of the farm 575 hours per week.
Find the amount of each crop that should be planted to maximize the profit.
The table below includes some additional, helpful information.
The objective of this particular problem is to maximize the profit.
Maximize the function:
over the region defined by the constraints.
First identify the variables and assumptions of the problem.

Now using the constraints formulate the linear programming model.
From here use computer implementation to solve using the simplex method.
Therefore, the optimal solution will occur when there are 510 acres of soy planted and 65 acres of oats.
The maximum profit at this solution will be, $223,500.
Example Question #7 : Math Modeling
A farm has 750 acres of land available for planting crops. The possible crops are soy, corn, and oats. There is 1,200 acre-ft of water for irrigation and the crew will be able to work of the farm 575 hours per week.
Find the amount of each crop that should be planted to maximize the profit.
The table below includes some additional, helpful information.
The objective of this particular problem is to maximize the profit.
Maximize the function:
over the region defined by the constraints.
First identify the variables and assumptions of the problem.

Now using the constraints formulate the linear programming model.
From here use computer implementation to solve using the simplex method.
Therefore, the optimal solution will occur when there are 343.182 acres of soy planted and 231.818 acres of corn planted.
The maximum profit at this solution will be, $230,454.50.
Certified Tutor
All Math Modeling Resources