All High School Math Resources
Example Questions
Example Question #85 : Triangles
You have two right triangles that are similar. The base of the first is 6 and the height is 9. If the base of the second triangle is 20, what is the height of the second triangle?
25
23
30
33
35
30
Similar triangles are proportional.
Base1 / Height1 = Base2 / Height2
6 / 9 = 20 / Height2
Cross multiply and solve for Height2
6 / 9 = 20 / Height2
6 * Height2= 20 * 9
Height2= 30
Example Question #1 : Right Triangles
In the figure above, line segments DC and AB are parallel. What is the perimeter of quadrilateral ABCD?
95
80
90
75
85
85
Because DC and AB are parallel, this means that angles CDB and ABD are equal. When two parallel lines are cut by a transversal line, alternate interior angles (such as CDB and ABD) are congruent.
Now, we can show that triangles ABD and BDC are similar. Both ABD and BDC are right triangles. This means that they have one angle that is the same—their right angle. Also, we just established that angles CDB and ABD are congruent. By the angle-angle similarity theorem, if two triangles have two angles that are congruent, they are similar. Thus triangles ABD and BDC are similar triangles.
We can use the similarity between triangles ABD and BDC to find the lengths of BC and CD. The length of BC is proportional to the length of AD, and the length of CD is proportional to the length of DB, because these sides correspond.
We don’t know the length of DB, but we can find it using the Pythagorean Theorem. Let a, b, and c represent the lengths of AD, AB, and BD respectively. According to the Pythagorean Theorem:
a2 + b2 = c2
152 + 202 = c2
625 = c2
c = 25
The length of BD is 25.
We now have what we need to find the perimeter of the quadrilateral.
Perimeter = sum of the lengths of AB, BC, CD, and DA.
Perimeter = 20 + 18.75 + 31.25 + 15 = 85
The answer is 85.
Example Question #86 : Triangles
A right triangle is defined by the points (1, 1), (1, 5), and (4, 1). The triangle's sides are enlarged by a factor of 3 to form a new triangle. What is the area of the new triangle?
None of the answers are correct
108 square units
36 square units
81 square units
54 square units
54 square units
The points define a 3-4-5 right triangle. Its area is A = 1/2bh = ½(3)(4) = 6. The scale factor (SF) of the new triangle is 3. The area of the new triangle is given by Anew = (SF)2 x (Aold) =
32 x 6 = 9 x 6 = 54 square units (since the units are not given in the original problem).
NOTE: For a volume problem: Vnew = (SF)3 x (Vold).
Example Question #1 : Right Triangles
Solve for 
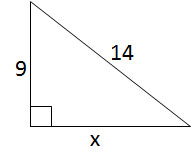
We will use the Pythagorean Theorem to solve for the missing side length.
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A square boxing ring has a perimeter of 






Since the perimeter of the ring is 

The distance between the two boxers in opposing corners is a straight line from any one corner to the other. That straight line forms the hypotenuse of a right triangle whose other two sides are each 
Solving for the length of the hypotenuse of this right triangle with the pythagorean theorem 
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
Given a right triangle with a leg length of 6 and a hypotenuse length of 10, find the length of the other leg, x.

4
8
16
64
8
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 62 = 102
Now we solve for x:
x2 + 36 = 100
x2 = 100 – 36
x2 = 64
x = 8
Also note that this is proportionally a 3/4/5 right triangle, which is very common. Always look out for a side-to-hypoteneuse ratio of 3/5 or 4/5, or a side-to-side ratio of 3/4, in any right triangle, so that you may solve such triangles rapidly.
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
In a right triangle a hypotenuse has a length of 8 and leg has a length of 7. What is the length of the third side to the nearest tenth?
Using the pythagorean theorem, 82=72+x2. Solving for x yields the square root of 15, which is 3.9
Example Question #82 : Triangles
Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

6
2
4
10
√8
2
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 22 = (√8)2 = 8
Now we solve for x:
x2 + 4 = 8
x2 = 8 – 4
x2 = 4
x = 2
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
The legs of a right triangle are 

Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
Example Question #2 : Right Triangles
Use the Pythagorean theorem: 
We know the length of one side and the hypotenuse.
Now we can solve for the missing side.
Certified Tutor
Certified Tutor
All High School Math Resources






















 .
.











