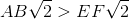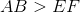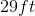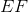Right Triangles
Help Questions
Math › Right Triangles
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
Explanation
The fence is going around the garden, so this is a perimeter problem.
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
30m
45m
35m
40m
25m
Explanation
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m

The above diagram depicts trapezoid 
(a)
(b)
(a) and (b) are equal.
(a) is greater.
(b) is greater.
It is impossible to tell from the information given.
Explanation





The Same-Side Interior Angles Theorem states that if two parallel lines are crossed by a transversal, then the sum of the measures of a pair of same-side interior angles is always 
Therefore, 

In the figure above, 



Explanation
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
One side of a regular hexagon is 20% shorter than one side of a regular pentagon. Which is the greater quantity?
(A) The perimeter of the pentagon
(B) The perimeter of the hexagon
(A) is greater
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(B) is greater
Explanation
Let 

Each side of the hexagon is 20% less than this length, or

The perimeter is five times this, or 
Since 


The sum of the lengths of three sides of a regular pentagon is one foot. Give the perimeter of the pentagon in inches.
It is impossible to determine the perimeter from the information given.
Explanation
A regular pentagon has five sides of the same length.
One foot is equal to twelve inches; since the sum of the lengths of three of the congruent sides is twelve inches, each side measures

The perimeter is

A rectangle is two feet longer than it is wide; its perimeter is 11 feet. What is its area in square inches?
It is impossible to determine the area from the information given
Explanation
The length of the rectangle is 2 feet, or 24 inches, greater than the width, so, if 

The perimeter of the rectangle is 11 feet, or 

The width is 21 inches, and the length is 45 inches. The area is their product:

One side of a regular pentagon is 20% longer than one side of a regular hexagon. Which is the greater quantity?
(A) The perimeter of the pentagon
(B) The perimeter of the hexagon
(A) and (B) are equal
(B) is greater
(A) is greater
It is impossible to determine which is greater from the information given
Explanation
Let 

Each side of the pentagon is 20% greater than this length, or

The perimeter is five times this, or 
The perimeters are the same.



Which is the greater quantity?
(a) The perimeter of
(b) The perimeter of
It is impossible to tell from the information given.
(a) and (b) are equal.
(a) is greater.
(b) is greater.
Explanation
No information is given about the legs of either triangle; therefore, no information about their perimeters can be deduced.





Which is the greater quantity?
(a)
(b)
(a) is greater.
(b) is greater.
(a) and (b) are equal.
It is impossible to tell from the information given.
Explanation
Each right triangle is a 
Since 



By the