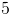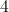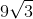All High School Math Resources
Example Questions
Example Question #1 : Triangles
If the hypotenuse of a triangle is 5 meters, which of the following is the closest value to the area of the triangle?
5
54
26
12
45
12
The answer is 12. In this circumstance, the area of the triangle cannot be smaller than its hypotenuse length, and cannot be bigger than its hypotenuse squared (that would be the area of a square).
Example Question #91 : Right Triangles
Triangle ABC is drawn between the points A(4, 3), B(4, 8), and C(7, 3). What is the area of ABC?
Drawing a quick sketch of this triangle will reveal that it is a right triangle. The lines AB and AC form the height and base of this triangle interchangeably, depending on how you look at it.
Either way the formula for the area of the triangle is the distance from A to B multiplied by the distance from A to C, divided by 2.
This is
Example Question #181 : Triangles

If 


The formula for area of a triangble is 
Since 


Plug in our given values to solve:
Example Question #1 : How To Find The Area Of A Right Triangle
Find the area of the following triangle:

The formula for the area of a right triangle is:
where 

Use the formulas for a a 


Our 
Plugging in our values, we get:
Example Question #2 : How To Find The Area Of A Right Triangle
Find the area of the following right triangle:

The formula for the area of a right triangle is:
where 

Use the formulas for a 

Our 
Plugging in our values, we get:
Example Question #1 : How To Find The Area Of A Right Triangle
You are given a right triangle with legs of length 







Since we have a right triangle, and are given the lengths of the legs, we are by definition given the base and height. Recall that the legs of the triangle are those next to the right angle, and the hypotenuse is across from the right angle.
Recall the formula for the area of a triangle:
Since we know the base and height we plug them into the equation above:
We are given units of feet, so the area will be in terms of square feet. Then, our answer is 
Example Question #2 : How To Find The Area Of A Right Triangle
The ratio for the side lengths of a right triangle is 3:4:5. If the perimeter is 48, what is the area of the triangle?
50
108
240
96
48
96
We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.
Example Question #1 : How To Find The Area Of A Right Triangle
The length of one leg of an equilateral triangle is 6. What is the area of the triangle?
The base is equal to 6.
The height of an quilateral triangle is equal to 

Example Question #1 : Triangles
Acute angles x and y are inside a right triangle. If x is four less than one third of 21, what is y?
3
7
90
18
87
87
We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.
Solve for x to find y.
One third of 21 is 7. Four less than 7 is 3. So if angle x is 3 then that leaves 87 for angle y.
Example Question #21 : Geometry
If a right triangle has one leg with a length of 4 and a hypotenuse with a length of 8, what is the measure of the angle between the hypotenuse and its other leg?
45
90
65
60
30
30
The first thing to notice is that this is a 30o:60o:90o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.
Certified Tutor
All High School Math Resources