Mathematical Relationships and Basic Graphs
Help Questions
Math › Mathematical Relationships and Basic Graphs
Given the sequence ![[3,9,27,...]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/864599/gif.latex)
Explanation
The formula for geometric sequences is defined by:
The term 


Substitute the known values.
To determine the seventh term, simply substitute 
The answer is:
Evaluate:
Explanation
To raise 






Solve the following:
Explanation
When the base isn't explicitly defined, the log is base 10. For our problem, the first term
is asking:
For the second term,
is asking:
So, our final answer is
Rewrite the following radical as an exponent:
Explanation
In order to rewrite a radical as an exponent, the number in the radical that indicates the root, gets written as a fractional exponent. Distribute the exponent to both terms by multiplying it by the exponents of each term as shown below:
From this point simplify the exponents accordingly:
Solve:
Explanation
Change the base of the inner term or log to base ten.
According to the log property:
The log based ten and the ten to the power of will cancel, leaving just the power.
The answer is:
Solve the equation:
Explanation
Subtract six from both sides.
Simplify both sides.
Cube both sides to eliminate the cube root.
Divide by three on both sides.
The answer is:
Add the fractions:
Explanation
Find the least common denominator to these fractions.
Multiply both denominators together.
Convert the fractions using this denominator.
The answer is:
Solve:
Explanation
Change the base of the inner term or log to base ten.
According to the log property:
The log based ten and the ten to the power of will cancel, leaving just the power.
The answer is:
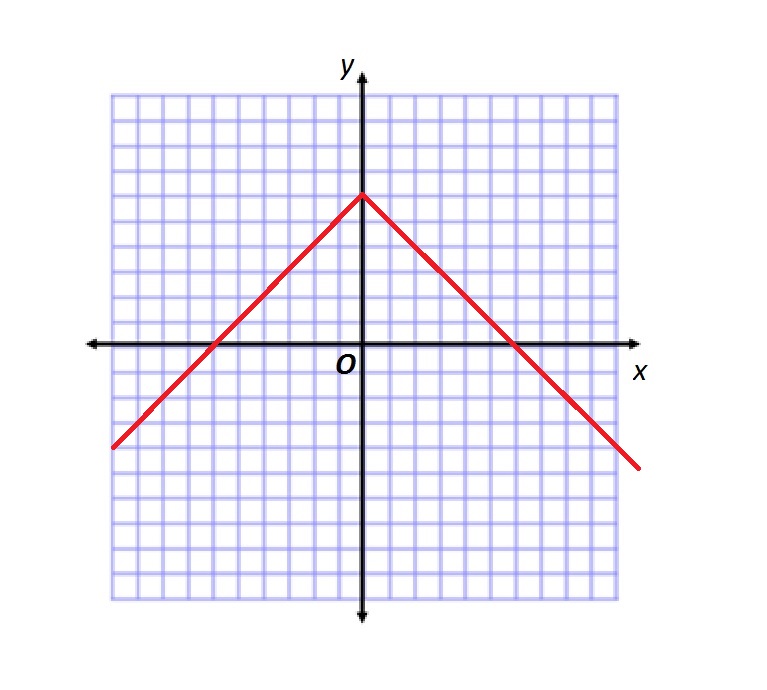
Refer to the above figure.
Which of the following functions is graphed?
Explanation
Below is the graph of 

The given graph is the graph of 



The function graphed is therefore
Simplify:
Explanation
When exponents with the same base are multiplied together, we we will simply add the exponents and keep the base the same.
Multiply:



























![\sqrt[3]{y^{3}z^{7}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/752020/gif.latex)




![\sqrt[3]{y^{3}z^{7}}=(y^{3}z^{7})^{\frac{1}{3}}=y^{\frac{3}{3}}z^{\frac{7}{3}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/752021/gif.latex)











![\sqrt[3]{3x}+6=8](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/795803/gif.latex)





![\sqrt[3]{3x}+6-6=8-6](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/795804/gif.latex)
![\sqrt[3]{3x} = 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/795805/gif.latex)



























