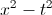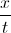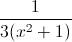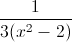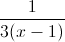All GRE Math Resources
Example Questions
Example Question #1 : How To Divide Rational Expressions
Which of the following is equivalent to 
We will need to simplify the expression . We can think of this as a large fraction with a numerator of


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

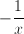


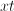
In order to convert the fraction 
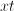

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction . We will now rewrite the numerator:
=
To simplify this further, we can think of 


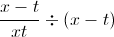
Lastly, we will use the property of exponents which states that, in general, 
The answer is 
Example Question #2405 : Act Math
Simplify:
Multiply by the reciprocal of 
Factor
Divide by common factors.
Example Question #1 : How To Divide Rational Expressions
Solve for 
To tackle this problem, you need to invert and multiply:
Here we see that we have created a quadratic equation. Therefore, we get all terms to one side, set it equal to zero and use the quadratic formula to solve.

The quadratic formula is:

Plugging these values in we get the following:
Example Question #2 : How To Divide Rational Expressions
Express the following as a single rational expression:
To divide one rational expression by another, invert and multiply:
Remember to foil the numerator meaning, multiply the first components of each binomial. Then multiply the outer components of each binomial. After that, multiply the inner components together, and lastly, multiply the components in the last position of the binomials together.
This arrives at the following:
You can't factor anything out, so that's your final answer.
All GRE Math Resources