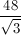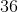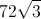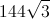All GRE Math Resources
Example Questions
Example Question #4 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

What is a possible value for the length of the missing side?
For a triangle where the length of two sides, 


For the triangle given:

Both choices A and B satisfy this criteria.
Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
A triangle has sides of lengths 
Quantity A: The length of the missing side.
Quantity B:
The relationship cannot be determined.
Quantity B is greater.
The two quantities are equal.
Quantity A is greater.
Quantity A is greater.
If two sides of a triangle are known and all angles are unknown, the length of the third side is limited by the difference and sum of the other two sides.
The missing side must be greater than 
Quantity A is greater.
Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
The lengths of two sides of a triangle are 

Quantity A: The length of the missing side.
Quantity B:
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined.
The relationship cannot be determined.
Seeing the sides 


Since the angles are unknown, the side is bounded as follows:
There are plenty of potential lengths that fall above and below 
Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
A triangle has sides 
Quantity A: The length of the missing side.
Quantity B:
The relationship cannot be determined.
Quantity B is greater.
Quantity A is greater.
The two quantities are equal.
Quantity B is greater.
If two sides of a triangle are known and the angles of the triangle are unknown, the length of the missing side is limited by the difference and sum of the other two sides.
For a triangle with sides 


Quantity B is greater.
Example Question #1 : Equilateral Triangles
Find the perimeter of an equilateral triangle with a height of 
None of the answer choices are correct.
Perimeter is found by adding up all sides of the triangle. All sides in an equilateral triangle are equal, so we need to find the value of just one side to know the values of all sides.
The height of an equilateral triangle divides it into two equal 30:60:90 triangles, which will have side ratios of 1:2:√3. The height here is the √3 ratio, which in this case is equivalent to 8, so to get the length of the other two sides, we put 8 over √3 (8/√3) and 2 * 8/√3 = 16/√3, which is the hypotenuse of our 30:60:90 triangle.
The perimeter is then 3 * 16/√3, or 48/√3.
Example Question #2 : How To Find The Perimeter Of An Equilateral Triangle
If the height of an equilateral triangle is 
By having a height in an equilateral triangle, the angle is bisected therefore creating two 
The height is opposite the angle 
Side opposite 








Since each side is the same and there are three sides, we just multply the answer by three to get 
Example Question #3 : How To Find The Perimeter Of An Equilateral Triangle
If area of equilateral triangle is 
The area of an equilateral triangle is 
So let's set-up an equation to solve for 


The 

Then take square root on both sides and we get 


Example Question #2 : Equilateral Triangles
What is the length of a side of an equilateral triangle if the area is 
The area of an equilateral triangle is 
So let's set-up an equation to solve for 


The 

Then take square root on both sides and we get 
Example Question #3 : Equilateral Triangles
If the height of the equilateral triangle is 
By having a height in an equilateral triangle, the angle is bisected therefore creating two 
The height is opposite the angle 
Side opposite 







Example Question #2 : Equilateral Triangles
What is the area of an equilateral triangle with a base of 
An equilateral triangle can be considered to be 2 identical 30-60-90 triangles, giving the triangle a height of 
All GRE Math Resources