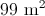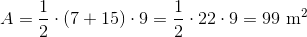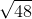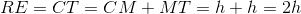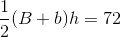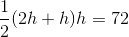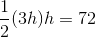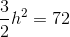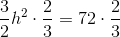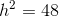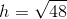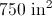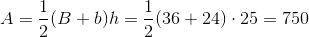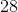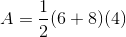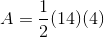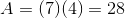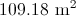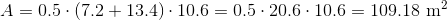How to find the area of a trapezoid
Help Questions
SSAT Middle Level Quantitative › How to find the area of a trapezoid
What is the area of a trapezoid with height 20 inches and bases of length 100 and 200?
Explanation
Set 


The area of a trapezoid can be found using this formula:
The area is 3,000 square inches.
Explanation
The area of a trapezoid is equal to the average of the length of the two bases multiplied by the height.
The formula to find the area of a trapezoid is:
In this problem, the lengths of the bases are 


Remember: the answer to the problem should have units in cm2 .
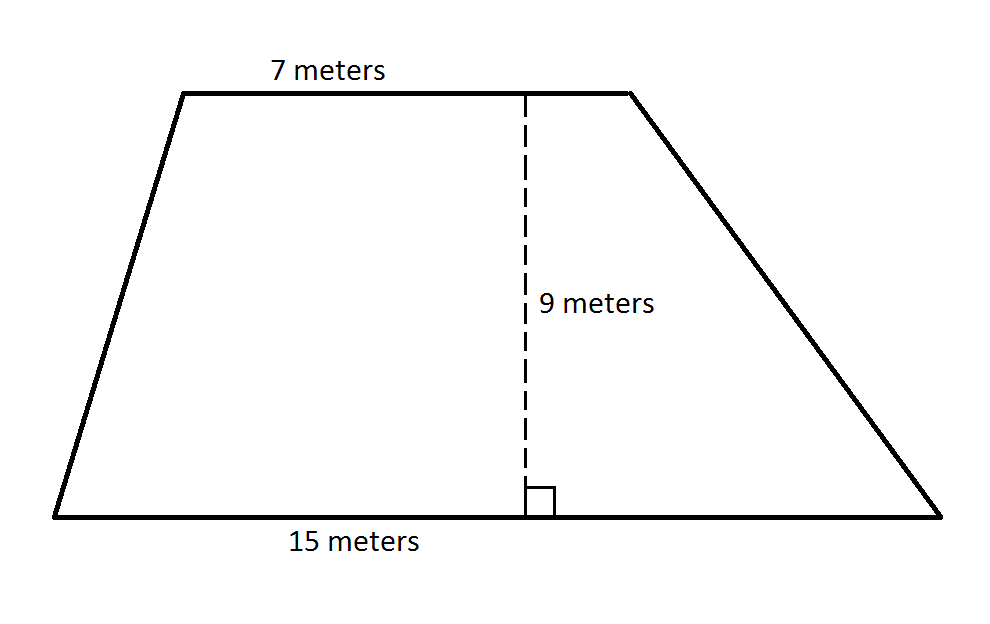
What is the area of the trapezoid?
Explanation
To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.
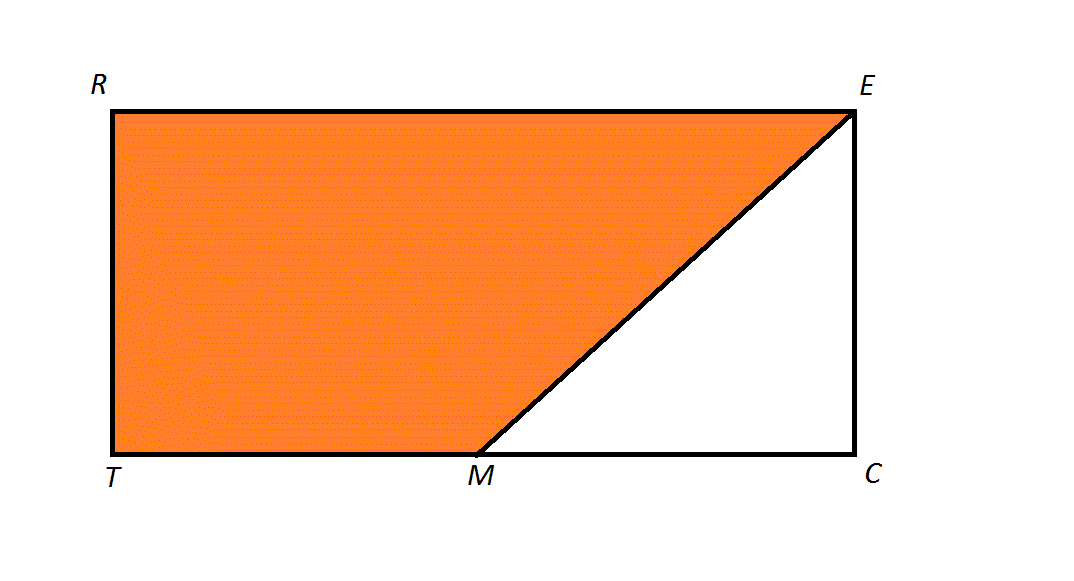
The above diagram depicts a rectangle 



More information is needed to answer this question.
Explanation
We can simplify this problem by supposing that the length of one leg of a triangle is 2. Then the other leg is 2, and the area of the triangle is
Since 



This makes the trapezoid one with height 2 and bases 2 and 4, so
The ratio of the area of the trapezoid to that of the triangle is 6 to 2, which simplifies to 3 to 1.

The above diagram depicts a rectangle 





Explanation
The length of a leg of 

Since the triangle is isosceles, then 



Therefore, the orange region is a trapezoid with bases 


This is the length of one leg of the triangle.
A trapezoid has a height of 


Explanation
Use the following formula, with 
Find the area of a trapezoid with a height of 


Explanation
The area 



Find the area of the trapezoid:
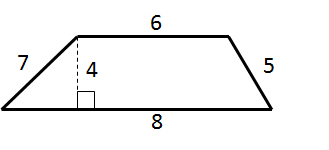
Explanation
The area of a trapezoid can be determined using the equation 
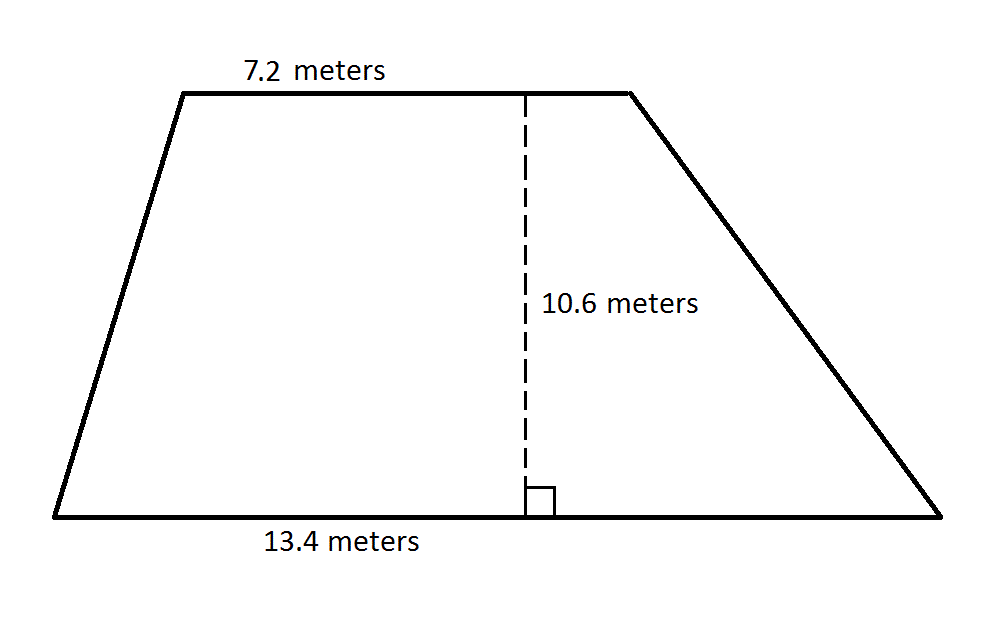
What is the area of the above trapezoid?
Explanation
To find the area of a trapezoid, multiply one half (or 0.5, since we are working with decimals) by the sum of the lengths of its bases (the parallel sides) by its height (the perpendicular distance between the bases). This quantity is
Find the area of a trapezoid with a height of 


Explanation
The area