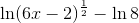Properties of Logarithms
Help Questions
Pre-Calculus › Properties of Logarithms
Condense the logarithm
Explanation
In order to condense the logarithmic expression, we use the following properties
As such
Completely expand this logarithm:
The answer is not present.
Explanation
We expand logarithms using the same rules that we use to condense them.
Here we will use the quotient property
and the power property
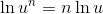
Use the quotient property:
Rewrite the radical:
Now use the power property:
Completely expand this logarithm:
The answer is not present.
Explanation
We expand logarithms using the same rules that we use to condense them.
Here we will use the quotient property
and the power property
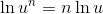
Use the quotient property:
Rewrite the radical:
Now use the power property:
Condense the logarithm
Explanation
In order to condense the logarithmic expression, we use the following properties
As such
Condense the following logarithmic equation:
Explanation
We start condensing our expression using the following property, which allows us to express the coefficients of two of our terms as exponents:
Our next step is to use the following property to combine our first three terms:
Finally, we can use the following property regarding subtraction of logarithms to obtain the condensed expression:
Condense the following logarithmic equation:
Explanation
We start condensing our expression using the following property, which allows us to express the coefficients of two of our terms as exponents:
Our next step is to use the following property to combine our first three terms:
Finally, we can use the following property regarding subtraction of logarithms to obtain the condensed expression:
Solve the following logarithmic equation:
Explanation
In order to solve this equation, we must apply several properties of logarithms. First we notice the term on the left side of the equation, which we can rewrite using the following property:
Where a is the coefficient of the logarithm and b is some arbitrary base. Next we look at the right side of the equation, which we can rewrite using the following property for the addition of logarithms:
Using both of these properties, we can rewrite the logarithmic equation as follows:
We have the same value for the base of the logarithm on each side, so the equation then simplifies to the following:
Which we can then factor to solve for 
Express 
Explanation
Using the properties of logarithms, expand the logrithm one step at a time:
When expanding logarithms, division becomes subtration, multiplication becomes division, and exponents become coefficients.

What is 
Explanation
Using the properties of logarithms,
the expression can be rewritten as
which simplifies to 
Express 
Explanation
Using the properties of logarithms, expand the logrithm one step at a time:
When expanding logarithms, division becomes subtration, multiplication becomes division, and exponents become coefficients.