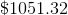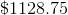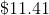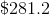All GRE Math Resources
Example Questions
Example Question #181 : Exponents
A five-year bond is opened with 

Each year, you can calculate your interest by multiplying the principle (

For two years, it would be:

Therefore, you can solve for a five year period by doing:
Using your calculator, you can expand the 


Example Question #1 : How To Find Compound Interest
Jack has 



First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).
Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:
Plug in the values given:
Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:
Add the two together, and we see that Jack makes a total of, 
Example Question #1 : How To Find Compound Interest
If a cash deposit account is opened with 

It is easiest to break this down into steps. For each year, you will multiply by 
After year 1: 
After year 2: 

After year 3: 

Thus, the positive difference of the interest from the last period and the interest from the first period is:
All GRE Math Resources