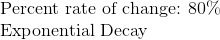All Common Core: High School - Functions Resources
Example Questions
Example Question #141 : Interpreting Functions
Determine the percent rate of change and whether the function represents exponential growth or decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.Math.content.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential growth.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #2 : Properties Of Exponents: Ccss.Math.Content.Hsf If.C.8b
Find the percent rate of change for the following function.
Identify whether the function is exponential growth or exponential decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.Math.content.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential decay.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #3 : Properties Of Exponents: Ccss.Math.Content.Hsf If.C.8b
Determine the percent rate of change for the following function.
Does the function represent an exponential growth or decay?
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential decay.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #4 : Properties Of Exponents: Ccss.Math.Content.Hsf If.C.8b
Determine the percent rate of change and whether the function represents exponential growth or decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.Math.content.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential growth.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #5 : Properties Of Exponents: Ccss.Math.Content.Hsf If.C.8b
Determine the percent rate of change and whether the function represents exponential growth or decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential growth.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #6 : Properties Of Exponents: Ccss.Math.Content.Hsf If.C.8b
Determine the percent rate of change and whether the function represents exponential growth or decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential growth.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #151 : High School: Functions
Determine the percent rate of change and whether the function represents exponential growth or decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential growth.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #152 : High School: Functions
Determine the percent rate of change and whether the function represents exponential growth or decay.
This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Calculate the percent rate of change.
Recall that 

Step 4: Answer question.
Following the above steps to solve this particular question, results in the following.
Step 1: Identify what the question is asking for.
Find whether the given function is exponential growth or decay after which, find the percent rate of change.
Step 2:
Use algebraic techniques to aid in solving the problem.
Given the function,
use the above expressions to help solve.
Since
the functions can be defined as exponential growth.
Step 3: Calculate the percent rate of change.
From the previous step it was found that,
therefore to solve for percent rate of change multiply by 100.

Step 4: Answer question.
Example Question #1 : Properties Of Exponents: Ccss.Math.Content.Hsf If.C.8b
A savings account has an interest rate of 


This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change and function values at specific input values.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
The question is asking for the Bob's account balance after 6 years.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Identify what is known.
Step 4: Substitute the known values into the growth function.
Example Question #154 : High School: Functions
Janet has a student loan of 

This question is testing one's ability to use properties of exponents to solve and interpret functions as well as identify key concepts of exponential growth and decay such as percent rate of change and function values at specific input values.
For the purpose of Common Core Standards, properties of exponents to interpret functions falls within the Cluster C of analyze functions using different representations concept (CCSS.MATH.CONTENT.HSF-IF.C.8).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
The question is asking for the amount of interest that will be added to the loan after two years.
Step 2: Use algebraic techniques to aid in solving the problem.
I. 
II. 
Step 3: Identify what is known.
Step 4: Substitute the known values into the growth function.
Step 5: Calculate the amount of interest.
To calculate the amount of interest, subtract the initial amount from the final amount found in step 4.
All Common Core: High School - Functions Resources