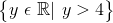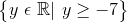All Common Core: High School - Functions Resources
Example Questions
Example Question #1 : High School: Functions
What is the range of function 
This question is testing the concept and understanding of a function's range. It is important to recall that range can be identified graphically or algebraically. Graphically, range contains the y-values that span the image of the function where as domain, contains the x-values of the function. Algebraically, range is known as the output y of a function when input x, is used. In other words, the input values when placed into the function results in the y values creating an (x, y) pair.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1. Identify the function and what the question is asking.
Find the range of the function.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the vertex of the function and using the properties of polynomials determine the range.
For this particular function let's use the third option to find the range.
Solving the quadratic equation to find the range algebraically requires the understanding that the vertex of a parabola represents either the peak (maximum) of a function or the valley (minimum) of the function.
Recall that a quadratic function can be written in the form,
and the formula to find the vertex x value is,

Finally to find the y value of the vertex we will substitute the x value found above into the original function. If the quadratic has a positive 

Step 3: Use algebraic technique to solve the problem.
First, identify the values of the variables.
Next, plug the values into the formula to find the vertex.
Now, substitute the x value found into the function to find the y output value.
Step 4: Interpret the solution to answer the question.
This question is asking for the range of the function. Using the formula to find the vertex and the properties of quadratics, it was discovered that the vertex is the valley of the function. This means that all other outputs will be greater than the vertex. Therefore, the range will be all real values of y for which y is greater than or equal to negative four. In mathematical terms this is represented by the following.
Example Question #1 : High School: Functions
What is the domain and range of the function 
This question is testing the concept and understanding of a function's domain. It is important to recall that domain can be identified graphically or algebraically. Graphically, range contains the y-values that span the image of the function where as domain, contains the x-values of the function. Algebraically, domain is known as the input values x of a function that then results in the y outputs. In other words, the input values when placed into the function results in the y values creating an (x, y) pair. It is also critical to understand that there are two important restrictions on domain. These restrictions occur when the x variable is in the denominator of a function or under a radical. This is because a fraction does not exist when there is a zero in the denominator; if under the radical is negative it results in imaginary values.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the function and what the question is asking.
Find the domain (x values) and range (y values) of the function. This includes identifying points where x values do not result in a y value. At these points the domain does not exist.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the x values that do not exist, these will be areas that are not in the domain.
For this particular function let's use the third option to find the domain.
Any time there is a fraction set the denominator equal to zero and solve for x, this will be a value that x cannot equal since it is not in the domain. Also, anytime there is a radical set the radicand equal to zero and solve for x; this will also be a value x cannot equal as it is also not in the domain.
Fractions:
Radicals
Step 3: Use algebraic technique to solve the problem.
For this particular function there exists a fraction and a radical therefore, the denominator of the fraction needs to be set to zero and solve for x. Also the radicand needs to be set to zero and solve for x.
For the fraction, using algebraic manipulations we get:
For the radicand, using algebraic manipulations we get:
Interpret the results to identify the domain. Since we found the areas where the domain does not exist we can state the domain as all real values of x except the areas for which we found to not exist. It is important to understand that "all reals" refer to all numbers negative, positive, zero, fractions, and decimal values.
Since the function is linear, the x variable is singular, we know that the range is all real y values.
Therefore, the domain and range solution in mathematical terms is as follows.
Example Question #1 : High School: Functions
What is the range of the function 
This question is testing the concept and understanding of a function's range. It is important to recall that range can be identified graphically or algebraically. Graphically, range contains the y-values that span the image of the function where as domain, contains the x-values of the function. Algebraically, range is known as the output y of a function when input x, is used. In other words, the input values when placed into the function results in the y values creating an (x, y) pair.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1. Identify the function and what the question is asking.
Find the range of the function.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the vertex of the function and using the properties of polynomials determine the range.
For this particular function let's use the third option to find the range.
This function contains an absolute value and thus it is important to understand how an absolute value effects a function. The absolute value bars makes whatever the value is inside the bars, positive. Therefore the function can can be manipulated into the following.
Step 3: Use algebraic technique to solve the problem.
Since the question asks for range, and the 

Example Question #1 : High School: Functions
What is the domain of the function 
This question is testing the concept and understanding of a function's domain. It is important to recall that domain can be identified graphically or algebraically. Graphically, domain contains the x-values of the function where as range, contains the y-values that span the image of the function. Algebraically, domain is known as the input values x of a function that then results in the y outputs. In other words, the input values when placed into the function results in the y values creating an (x, y) pair. It is also critical to understand that there are two important restrictions on domain. These restrictions occur when the x variable is in the denominator of a function or under a radical. This is because a fraction does not exist when there is a zero in the denominator; if under the radical is negative it results in imaginary values.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the function and what the question is asking.
Find the domain (x values) of the function. This includes identifying points where x values do not result in a y value. At these points the domain does not exist.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the x values that do not exist, these will be areas that are not in the domain.
For this particular function let's use the third option to find the domain.
Any time there is a fraction set the denominator equal to zero and solve for x, this will be a value that x cannot equal since it is not in the domain. Also, anytime there is a radical set the radicand equal to zero and solve for x; this will also be a value x cannot equal as it is also not in the domain.
Fractions:
Radicals
Step 3: Use algebraic technique to solve the problem.
Since there is a fraction in the function that contains the variable in question, set the denominator equal to zero and solve for 
Perform algebraic operations to manipulate the equations and solve for the variable.
Let us rewrite this expression to represent what it truly means.
"

Example Question #1 : Interpreting Functions
What is the domain and range of the function 
This question is testing the concept and understanding of a function's domain. It is important to recall that domain can be identified graphically or algebraically. Graphically, range contains the y-values that span the image of the function where as domain, contains the x-values of the function. Algebraically, domain is known as the input values x of a function that then results in the y outputs. In other words, the input values when placed into the function results in the y values creating an (x, y) pair. It is also critical to understand that there are two important restrictions on domain. These restrictions occur when the x variable is in the denominator of a function or under a radical. This is because a fraction does not exist when there is a zero in the denominator; if under the radical is negative it results in imaginary values.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify what the question is asking for.
Find the domain (x values) and range (y values) of the function. This includes identifying points where x values do not result in a y value. At these points the domain does not exist.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the x values that do not exist, these will be areas that are not in the domain.
For this particular function let's use the third option to find the domain.
Any time there is a fraction set the denominator equal to zero and solve for x, this will be a value that x cannot equal since it is not in the domain. Also, anytime there is a radical set the radicand equal to zero and solve for x; this will also be a value x cannot equal as it is also not in the domain.
Fractions:
Radicals
Step 3: Use algebraic technique to solve the problem.
Let us first find the domain by calculating the points where the function does not exist. Since there is a radical in the numerator, set the inside portion (radicand) greater than or equal to zero and solve. There is also a variable in the denominator, therefore the denominator will also need to be set to zero and the variable solved for.
Let us first deal with the radical:
Any number less than two and greater than negative two will create a negative value under the radical which will create a imaginary value and thus is not in the domain.
Now let us deal with the fraction:
Step 4: Graph the function to find the range.

Remembering that the range of a function is represented by the 
Step 5: Answer the question.
Example Question #1 : High School: Functions
What is the domain of the function 
This question is testing the concept and understanding of a function's domain. It is important to recall that domain can be identified graphically or algebraically. Graphically, domain contains the x-values of the function where as range, contains the y-values that span the image of the function. Algebraically, domain is known as the input values x of a function that then results in the y outputs. In other words, the input values when placed into the function results in the y values creating an (x, y) pair. It is also critical to understand that there are two important restrictions on domain. These restrictions occur when the x variable is in the denominator of a function or under a radical. This is because a fraction does not exist when there is a zero in the denominator; if under the radical is negative it results in imaginary values.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the function and what the question is asking.
Find the domain (x values) of the function. This includes identifying points where x values do not result in a y value. At these points the domain does not exist.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the x values that do not exist, these will be areas that are not in the domain.
For this particular function let's use the third option to find the domain.
Any time there is a fraction set the denominator equal to zero and solve for x, this will be a value that x cannot equal since it is not in the domain. Also, anytime there is a radical set the radicand equal to zero and solve for x; this will also be a value x cannot equal as it is also not in the domain.
Fractions:
Radicals
Step 3: Use algebraic technique to solve the problem.
Since there is a fraction in the function that contains the variable in question, set the denominator equal to zero and solve for 
Therefore, the domain of the function is all real values of 
Step 4: Verify solution graphically.

The graph above depicts a vertical asymptote at 
Example Question #1 : High School: Functions
What is the range of the function 
This question is testing the concept and understanding of a function's range. It is important to recall that range can be identified graphically or algebraically. Graphically, range contains the y-values that span the image of the function where as domain, contains the x-values of the function. Algebraically, range is known as the output y of a function when input x, is used. In other words, the input values when placed into the function results in the y values creating an (x, y) pair.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.MATH.CONTENT.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1. Identify the function and what the question is asking.
Find the range of the function.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the vertex of the function and using the properties of polynomials determine the range.
For this particular function let us use option I to solve.
Step 3: Using technology resource graph the function and interpret it.

Remember that the range contains all 

In mathematical terms the solution is,

Example Question #7 : Interpreting Functions
What is the domain of the function 
This question is testing the concept and understanding of a function's domain. It is important to recall that domain can be identified graphically or algebraically. Graphically, domain, contains the x-values of the function where as the range contains the y-values that span the image of the function. Algebraically, range is known as the output y of a function when domain (input) x, is used. In other words, the input values when placed into the function results in the y values creating an (x, y) pair.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.MATH.CONTENT.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1. Identify the function and what the question is asking.
Find the domain of the function.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the vertex of the function and using the properties of polynomials determine the range.
For this particular function let us use option III to simplify the function then use technology to help solve for its domain.
To simplify this function, factor out a common factor of 

Step 3: Use technology to graph the simplified function.

Interpreting the above graph for the domain requires examination of the x values. It is seen above that any x value can be inputed into the function and results in an existing y value output. This means that the domain is all real x values. In mathematical terms,

Example Question #8 : Interpreting Functions
What is the domain of the function 
This question is testing the concept and understanding of a function's domain. It is important to recall that domain can be identified graphically or algebraically. Graphically, domain contains the x-values of the function where as range, contains the y-values that span the image of the function. Algebraically, domain is known as the input values x of a function that then results in the y outputs. In other words, the input values when placed into the function results in the y values creating an (x, y) pair. It is also critical to understand that there are two important restrictions on domain. These restrictions occur when the x variable is in the denominator of a function or under a radical. This is because a fraction does not exist when there is a zero in the denominator; if under the radical is negative it results in imaginary values.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.Math.content.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the function and what the question is asking.
Find the domain (x values) of the function. This includes identifying points where x values do not result in a y value. At these points the domain does not exist.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the x values that do not exist, these will be areas that are not in the domain.
For this particular function let's use the third option to simplify the function and then use the first option to graph and solve for the domain.
To simplify this function factor out a common factor of 
Any time there is a fraction set the denominator equal to zero and solve for x, this will be a value that x cannot equal since it is not in the domain.
Fractions:
Step 3: Use algebraic technique along with graphing the function to solve the problem.
Graph to verify solution.

The graph above shows the function to have a vertical asymptote at 
Thus the solution to this problem is,
Example Question #9 : Interpreting Functions
What is the range of the function 
This question is testing the concept and understanding of a function's range. It is important to recall that range can be identified graphically or algebraically. Graphically, range contains the y-values that span the image of the function where as domain, contains the x-values of the function. Algebraically, range is known as the output y of a function when input x, is used. In other words, the input values when placed into the function results in the y values creating an (x, y) pair.
For the purpose of Common Core Standards, domain and range fall within the Cluster A of the function and use of function notation concept (CCSS.MATH.CONTENT.HSF-IF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1. Identify the function and what the question is asking.
Find the range of the function.
Step 2. Discuss the options to solve the problem.
I. Graphically plot the function by computer/technology resource. Then interpret the graph.
II. Create a table of (x, y) pairs and plot the points to create the graph. Then interpret the graph.
III. Algebraically find the vertex of the function and using the properties of polynomials determine the range.
For this particular function let us use option I to solve.
Step 3: Using technology resource graph the function and interpret it.

Remember that the range contains all 

In mathematical terms the solution is,

All Common Core: High School - Functions Resources