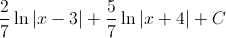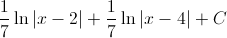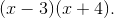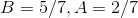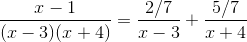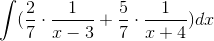Integrals
Help Questions
AP Calculus BC › Integrals
Find the volume of the solid generated by rotating about the y-axis the region under the curve 


None of the other answers
Explanation
Since we are revolving a function of 
Using the formula for cylindrical shells, we have

Find the volume of the solid generated by rotating about the y-axis the region under the curve 


None of the other answers
Explanation
Since we are revolving a function of 
Using the formula for cylindrical shells, we have

Find the volume of the solid generated by rotating about the y-axis the region under the curve 


None of the other answers
Explanation
Since we are revolving a function of 
Using the formula for cylindrical shells, we have

Explanation
Evaluate
Explanation
Use the fundamental theorem of calculus to evaluate:
Explanation
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
Explanation
Explanation
Evaluate
Explanation
Use the fundamental theorem of calculus to evaluate:
Explanation
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 






![=[2\pi x^{5/2}]^{4}_{0}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/604752/gif.latex)





![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{0}^{12}(11sin(20sin(x)))dx\&\text{So the interval is }[0,12]\text{ the subintervals have length }\frac{12-(0)}{3}=4\&\text{and since we are using the *left*point of each interval, the x-values are:}\&[0,4,8]\&\int_{0}^{12}(11sin(20sin(x)))dx=4[(0)+(11sin(20sin(4)))+(11sin(20sin(8)))]\&\int_{0}^{12}(11sin(20sin(x)))dx=11.66\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/932978/gif.latex)






![\frac{1}{3} (6-3)^3 - [ \frac{1}{3}(0-3)^3] = \frac{1}{3} (3)^3 - \frac{1}{3} (-3)^3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/854677/gif.latex)