Force Diagrams
Help Questions
AP Physics 1 › Force Diagrams

A mass is suspended by two cables. What is the magnitude of the tension in the left cable?
Explanation
Begin by diagraming the forces acting on the mass in the problem:

The mass itself creates a force due to gravity in the downward direction:
For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:
The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:
Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:
A block of mass 




What is the value of 




Explanation

The free body diagram of the block is given above. This block has three forces acting on it. First, it's weight under the influence of gravity, which is given as 






Now we can use Newton's 2nd law to relate the given forces above. Newton's 2nd law gives us two equations:

Because the block is constrained to move along the surface of the inclined plane, there should be no acceleration in the y direction, and so 


Summing all the forces in the x-direction gives us
Summing all the forces in the y-direction gives us
Plugging these values into the force equations above gives us the following equations:
Solving for 



Now we solve the equation for 

Now we divide each side by 
The final result is obtained by canceling the 
Therefore we arrive at the conclusion that
A ball with mass 

Find the magnitude of the ball's normal force.
Explanation
The normal force is perpendicular to the plane:

First, we need to find 
We can solve for 



Rearranging to solve this equation for 
Substituting in the side lengths of the given triangle, we can solve for 
Note that the normal force is one of the legs of another right triangle. The other leg is the parallel force, and the hypotenuse is the force of gravity.
Using trigonometry, we know that
because 

Substituting in the known values into this equation, we can solve for the normal force:
Jennifer and Jessica are lifting a heavy box. If the box has a mass of 


Explanation
Solving for
Plugging in values
A 




Explanation
Conservation of momentum gives that the angular momentum of the golf swing is transferred into linear momentum for the ball, or that 

Using kinematics, we know that 

Kinetic friction can be expressed as 

Plugging in known values and solving for 

If three locomotives are pulling a 

Explanation
Using
Converting 

A 


Explanation
The tensions in both ropes are caused by the bucket being pulled down by gravity, hence the only relevant forces acting in this scenario are those in the y-direction. Since the bucket is being held up against gravity, the upward forces should balance exactly with the downward forces. The forces in the y-direction can be balanced like this:


Two forces are exerted on the center of an object. What angle between the two forces would provide the largest resultant force?
Explanation
Imagine two men of equal strength pulling on ropes that are connected to a crate. In order to obtain the largest resulting force the two men should pull in the same direction at 


A 

None of these
Explanation
As can be seen in the diagram, the force pushing down the ramp is equal to
The force pushing the object into the ramp is
The force into the ramp will be equal to the normal force, thus
The net force pushing the woman down the ramp is
At the moment she starts slipping, the net force is equal to zero
Solving for 
Consider the following system:
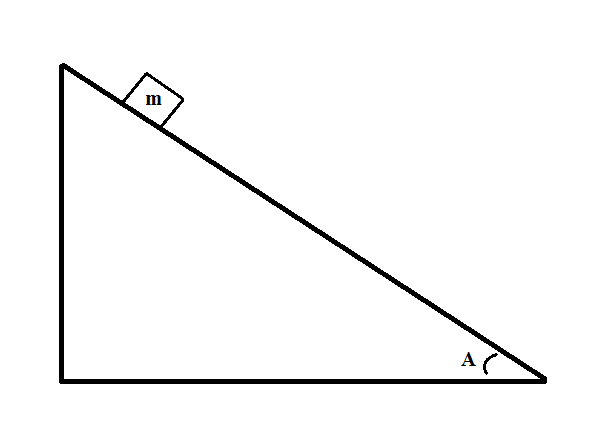
If the mass accelerates down the plane at a rate of 

Explanation
Before we start using equations, we need to determine what forces are acting on the block in this system. The only relevant forces in this situation are gravity and friction. We are given the acceleration of the block, giving us the tools to find the net force.
Using Newton's second law, we can write:
The force of friction is subtracted because it is in the opposite direction of the movement of the block. Substituting in expressions for each variable, we get:
Canceling out mass and rearranging for the coefficient of kinetic friction, we get:
We have values for each variable, allowing us to solve:


































































































