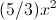All AP Calculus AB Resources
Example Questions
Example Question #171 : Functions, Graphs, And Limits
Find the derivative.
y = sec (5x3)
y' = –csc(5x3)cot(5x3)
y' = sec(5x3)tan(5x3)(15x2)
y' = –sec(5x3)tan(5x3)(15x2)
y' = sec(5x3)tan(5x3)
y' = –csc(5x3)cot(5x3)(15x2)
y' = sec(5x3)tan(5x3)(15x2)
The derivative of the function y = sec(x) is sec(x)tan(x). First take the derivative of the outside of the function: y = sec(4x3) : y' = sec(5x3)tan(5x3). Then take the derivative of the inside of the function: 5x3 becomes 15x2. So your final answer is: y' = ec(5x3)tan(5x3)15x2
Example Question #2 : Understanding The Limiting Process.
Find the slope of the tangent line to the graph of f at x = 9, given that f(x) = –x2 + 5√(x)
18 + (5/6)
–18
–18 + (5/6)
–18 – (5/6)
18
–18 + (5/6)
First find the derivative of the function.
f(x) = –x2 + 5√(x)
f'(x) = –2x + 5(1/2)x–1/2
Simplify the problem
f'(x) = –2x + (5/2x1/2)
Plug in 9.
f'(3) = –2(9) + (5/2(9)1/2)
= –18 + 5/(6)
Example Question #1 : Understanding The Limiting Process.
Find the derivative
(x + 1)/(x – 1)
(–2)/(x – 1)2
1
(–2)/(x + 1)2
(–2)/(x – 1)
(x + 1) + (x – 1)
(–2)/(x – 1)2
Rewrite problem.
(x + 1)/(x – 1)
Use quotient rule to solve this derivative.
((x – 1)(1) – (x + 1)(1))/(x – 1)2
(x – 1) – x – 1)/(x – 1)2
–2/(x – 1)2
Example Question #31 : Limits Of Functions (Including One Sided Limits)
Use the chain rule and the formula
Example Question #176 : Functions, Graphs, And Limits
Find the derivative of
The answer is 
Example Question #1 : Understanding The Limiting Process.
Differentiate 
Using the power rule, multiply the coefficient by the power and subtract the power by 1.
Example Question #2 : Understanding The Limiting Process.
Differentiate 
Use the product rule:
Example Question #41 : Limits Of Functions (Including One Sided Limits)
Differentiate:
Use the product rule to find the derivative of the function.
Example Question #42 : Limits Of Functions (Including One Sided Limits)
Differentiate:
The derivative of any function of e to any exponent is equal to the function multiplied by the derivative of the exponent.
Example Question #2 : Understanding The Limiting Process.
Find the second derivative of 
Factoring out an x gives you 
All AP Calculus AB Resources