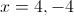All Algebra II Resources
Example Questions
Example Question #333 : Sat Subject Test In Math I
What is the horizontal asymptote of the graph of the equation 
The asymptote of this equation can be found by observing that 



So the value that 


Example Question #3 : Solving Exponential Functions
What is/are the asymptote(s) of the graph of the function


An exponential equation of the form 



Example Question #1 : Asymptotes
Find the vertical asymptote of the equation.
There are no vertical asymptotes.
To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.
Example Question #1 : Solving And Graphing Exponential Equations
Determine the asymptotes, if any:
Factorize both the numerator and denominator.
Notice that one of the binomials will cancel.
The domain of this equation cannot include 
The simplified equation is:
Since the 

Set the denominator equal to zero.
Subtract one from both sides.
There will be an asymptote at only:
The answer is:
Example Question #2 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions
Which of the choices represents asymptote(s), if any?
Factor the numerator and denominator.
Notice that the 

The denominator cannot be equal to zero. Set the denominator to find the location where the x-variable cannot exist.
The asymptote is located at 
Example Question #2 : Solving And Graphing Exponential Equations
Where is an asymptote located, if any?
Factor the numerator and denominator.
Rewrite the equation.
Notice that the 

Set the denominator equal to zero and solve for x.
An asymptote is located at:
The answer is:
Example Question #341 : Sat Subject Test In Math I
Consider the exponential function 
There is one vertical asymptote at 
There is one vertical asymptote at 
There is one horizontal asymptote at 
There are no asymptotes. 


There is one horizontal asymptote at 
For positive 










Example Question #51 : Functions And Graphs
Solve the equation for 
Begin by recognizing that both sides of the equation have a root term of 
Using the power rule, we can set the exponents equal to each other.
Example Question #1 : Solving Exponential Functions
Solve the equation for 
Begin by recognizing that both sides of the equation have the same root term, 
We can use the power rule to combine exponents.
Set the exponents equal to each other.
Example Question #3 : Solving And Graphing Exponential Equations
In 2009, the population of fish in a pond was 1,034. In 2013, it was 1,711.
Write an exponential growth function of the form 


Solve for the values of a and b:
In 2009, 




In 2013, 




![b=\sqrt[4]{\frac{1711}{1034}}\approx1.1342](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/220698/gif.latex)
Then the exponential growth function is

Certified Tutor
Certified Tutor
All Algebra II Resources