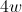All SSAT Middle Level Math Resources
Example Questions
Example Question #6 : How To Find The Area Of A Square

What is the total area of the surface of the cube shown in the above diagram?
A cube comprises six faces, each of which is a square. To find its total surface area, find the area of one face by squaring its sidelength:
Then multiply this by six:
Example Question #7 : How To Find The Area Of A Figure
A square is 9 feet long on each side. How many smaller squares, each 3 feet on a side can be cut out of the larger square?
Each side can be divided into three 3-foot sections. This gives a total of 
Example Question #2 : How To Find The Area Of A Square
Order the following from least area to greatest area:
Figure A: A square with sides of length 3 feet each.
Figure B: A rectangle with length 30 inches and width 42 inches.
Figure C: A rectangle with length 2 feet and width 4 feet.
Figure A has area 
Figure B has dimensions 


Figure C has area 
From least area to greatest, the figures rank C, B, A.
Example Question #5 : How To Find The Area Of A Square
The length of one side of a square is 
The area of any quadrilateral is found by multiplying the length by the width. Because a square has four equal sides, the length and width are the same. For the square in this question, the length and width are 
Remember: area is always given in units2 .
Example Question #43 : Geometry
If a square has a side that is 3 yards long, what is the area in square feet?
The area of a square is found by multiplying the length of a side by itself.
If one side is 3 yards, this means one side is 9 feet since there are 3 feet in a yard.
Since every side is of equal length, you would multiply 9 feet by 9 feet to find the area.
This results in 81 square feet, which is the correct answer.
Example Question #2134 : Hspt Mathematics

Note: Figure NOT drawn to scale.
Refer to the above diagram, which shows a square. Give the ratio of the area of the yellow region to that of the white region.
The correct answer is not given among the other choices.
The area of the entire square is the square of the length of a side, or

The area of the right triangle is half the product of its legs, or

The area of the yellow region is therefore the difference of the two, or

The ratio of the area of the yellow region to that of the white region is

Example Question #61 : Plane Geometry
Find the area of a square with a width of 13cm.
To find the area of a square, we will use the following formula:
where l is the length and w is the width of the square.
Now, we know the width of the square is 13cm. Because it is a square, all sides are equal. Therefore, the length is also 13cm.
So, we can substitute. We get
Example Question #1 : Rectangles
The width of a rectangle is half of its length. If the width is given as 

The sum of the widths is 


Example Question #2 : Rectangles

The above figure shows the size and shape of a yard that is to be surrounded by some fence. How many feet of fence will be needed?
Note: all sides meet at right angles.
The best way to see that 750 feet of fence are needed is to look at this augmented diagram.
Note that two of the sides are extended to form a smaller rectangle whose sides can be deduced by subtraction. Since opposite sides of a rectangle are congruent, this allows us to fill in the two missing sidelengths of the original figure.

Now add:
Example Question #3 : Rectangles

Give the perimeter of the rectangle in the above diagram.
The perimeter of a rectangle is the sum of the length and the width, multiplied by 2:
The rectangle has a perimeter of 38 centimeters.
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources