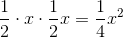All SSAT Middle Level Math Resources
Example Questions
Example Question #61 : Geometry
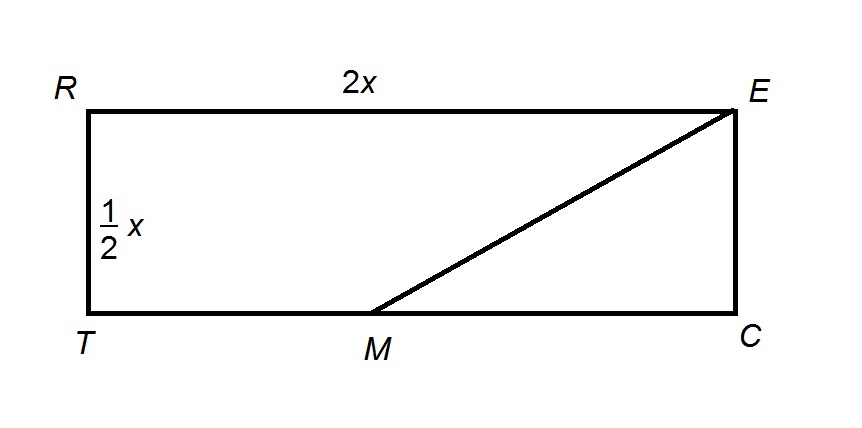
The above diagram shows Rectangle 


The area of 





Its area is half their product, or
Set this equal to 225:

Example Question #62 : Geometry
Find the area of a triangle with a height of 12in and a base that is half the height.
To find the area of a triangle, we will use the following formula:
where b is the base and h is the height of the triangle.
Now, we know the height of the triangle is 12in. We also know the base of the triangle is half of the height. Therefore, the base of the triangle is 6in.
So, we can substitute. We get
Example Question #63 : Geometry
Find the area of the triangle below

The equation for area of a triangle is

In this case the coordinates of the base are 

The coordinates of the side that determines the height are 
Therefore the height is 

Example Question #1 : How To Find Perimeter Of A Triangle
The perimeter of an isosceles triangle is 18. What is a possible list of the lengths of the sides?
Since it is isosceles, 2 of the sides must be equal. They must also add to 18.
Example Question #2 : How To Find Perimeter Of A Triangle
An equilateral triangle has perimeter 8 feet 6 inches. How long is one side?
3 feet 2 inches
2 feet 6 inches
2 feet 2 inches
3 feet 4 inches
2 feet 10 inches
2 feet 10 inches
One foot is equal to 12 inches, so the perimeter 8 feet 6 inches is equal to 
An equilateral triangle has three sides of equal measure, so divide its perimeter by 3:
To convert 34 inches to feet and inches:
One side measures 2 feet 10 inches.
Example Question #3 : How To Find Perimeter Of A Triangle
Find the perimeter of the triangle above.
Note: Figure not drawn to scale.
None of these answers are correct.
The perimeter of a shape is the length around the shape. In order to find the perimeter of a triangle, add the lengths of the sides: 
Because the lengths are in inches, the answer must be in inches as well.
Example Question #4 : How To Find Perimeter Of A Triangle
If the triangle below is an isosceles triangle, what of the following choices could be its perimeter?

12
21
19
20
15
19
An isosceles triangle has 2 equal sides and a third side that is unequal. If one given side is 5 and the other is 7, then the third missing side must equal either 5 or 7. If the missing side has length 5, then the perimeter is 17 (5+5+7). If the missing side is of length 7, then the perimeter is 19 (7+7+5). Of the two, only 19 is an answer choice, so the correct answer is 19.
Example Question #23 : Plane Geometry
The perimeter of equilateral triangle QRS is 4 times the perimeter of equilateral triangle TUV. If the perimeter of QRS is 36, what is the length of one side of TUV?
18
4
3
9
12
3
If the perimeter of QRS is 4 times the perimeter of TUV, and the perimeter of QRS is 36, then the perimeter of TUV is equal to 36 divided by 4, which is 9. If the perimeter of equilateral triangle TUV is 9, then each individual side must have length 3.
Example Question #2 : How To Find Perimeter Of A Triangle
What is the perimeter, in feet, of an equilateral triangle that has a side of 36 inches?
Given that there are 12 inches in a foot, 36 inches is equal to 3 feet because 36 divided by 12 equals 3.
In an equilateral triangle, each side is equal. Thus, if one side is 3 feet long, that means that each of the other two sides are also 3 feet long.
Add the sides together to find the total perimeter.
The perimeter of the triangle is 9 feet.
Example Question #4 : How To Find Perimeter Of A Triangle
The perimeter of an isosceles triangle is 19. What is the possible list of the lengths of the sides?
Since the triangle is an isoscles, two of the sides must be equal. They must also add to 

Plugging 

Therefore, the inequalities hold true thus, 
Therefore, 
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources