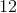All PSAT Math Resources
Example Questions
Example Question #1 : Other Polygons
A square has an area of 36 cm2. A circle is inscribed and cut out. What is the area of the remaining shape? Use 3.14 to approximate π.
7.74 cm2
15.48 cm2
28.26 cm2
3.69 cm2
12.14 cm2
7.74 cm2
We need to find the area of both the square and the circle and then subtract the two. Inscribed means draw within a figure so as to touch in as many places as possible. So the circle is drawn inside the square. The opposite is circumscribed, meaning drawn outside.
Asquare = s2 = 36 cm2 so the side is 6 cm
6 cm is also the diameter of the circle and thus the radius is 3 cm
A circle = πr2 = 3.14 * 32 = 28.28 cm2
The resulting difference is 7.74 cm2
Example Question #2 : Other Polygons
In the square above, the radius of each half-circle is 6 inches. What is the area of the shaded region?
144 – 36π
144 – 6π
36 – 9π
144 – 9π
36 – 6π
144 – 36π
We can find the area of the shaded region by subtracting the area of the semicircles, which is much easier to find. Two semi-circles are equivalent to one full circle. Thus we can just use the area formula, where r = 6:
π(62) → 36π
Now we must subtract the area of the semi-circles from the total area of the square. Since we know that the radius also covers half of a side, 6(2) = 12 is the full length of a side of the square. Squaring this, 122 = 144. Subtracting the area of the circles, we get our final terms,
= 144 – 36π
Example Question #91 : Plane Geometry
If square A has a side of length 5 inches, how many times bigger is the area of square B if it has a side of length 25 inches?
625 times
2 times
5 times
25 times
4 times
25 times
First find the area of both squares using the formula 
For square A, s = 5.
For square B, s = 25.
The question is asking for the ratio of these two areas, which will tell us how many times bigger square B is. Divide the area of square B by the area of square A to find the answer.
Example Question #92 : Plane Geometry

If Bailey paints the wall shaped like above and uses one bucket per 5 square units, how many buckets does Bailey need?
To solve, we will need to find the area of the wall. We can do this by finding the areas of each section and adding them together. Break the area into a rectange and two triangles.

The area of the rectangle will be equal to the base times the height. The area of each triangle will be one half its given base times its height.
For the rectangle, the base is 12 and the height is 4 (both given in the figure).
The triangle to the right has a given base of 6, but we need to solve for its height. The height will be equal to the difference between the total height (6) and the height of the rectangle (4).
We now have the base and height of the triangle to the right, allowing us to calculate its area.
Now we need to solve the triangle to the left. We solved for its height (2), but we still need to solve for its base. The total base of the rectangle is 12. Subtract the base of the right-side triangle (6) and the small segment at the top of the rectangle (3) from this total length to solve for the base of the left triangle.
The left-side triangle has a base of 3 and a height of 2, allowing us to calculate its area.
Add together the two triangles and the rectangle to find the total area.
We know that each bucket of paint will cover 5 square units, and we have 57 square units total. Divide to find how many buckets are required.
We will need 11 full buckets and part of a twelfth bucket to cover the wall, meaning that we will need 12 buckets total.
Example Question #93 : Plane Geometry
A square is inscribed within a circle with a radius 
First, find the area of the circle.
Next, find the length of 1 side of the square using the Pythagorean Theorem. Two radii from the center of the circle to adjacent corners of the square will create a right angle at the center of the circle. The radii will be the legs of the triangle and the side of the square will be the hypotenuse.
Find the area of the square.
Subtract the area of the square from the area of the circle.
Example Question #411 : Geometry

Refer to the above figure. Quadrilateral 





Polygon 


The area of 
The area of Square 
Add the areas:
This is the area of the polygon.
Example Question #3 : How To Find The Area Of A Polygon

Note: Figure NOT drawn to scale.
The above figure shows Rectangle 




What percent of Rectangle 
The area of 


The answer is independent of the sidelengths of the rectangle, so to ease calculations - this will become more apparent later - we will arbitrarily assign to the rectangle the dimensions
and, subsequently,
and, since 


The area of Rectangle 

Since 


The area of 

The area of 
The area of the shaded region is therefore 

Certified Tutor
Certified Tutor
All PSAT Math Resources