Solving Polynomial and Rational Inequalities
Help Questions
Pre-Calculus › Solving Polynomial and Rational Inequalities



Explanation
We begin by finding the zeros of the equation using the numerator.
So we know that the function will equal zero when 


And so the function is undefined at 
And if we graph these points we see something like below (which is our answer). Note that the dotted blue line is the vertical asymptote at 




Explanation
We begin by finding the zeros of the equation using the numerator.
So we know that the function will equal zero when 


And so the function is undefined at 
And if we graph these points we see something like below (which is our answer). Note that the dotted blue line is the vertical asymptote at 

Which of the following best describes the statement:
The undefined points of rational functions are vertical asymptotes.
The statement is always true
The statement is always false
The statement is true in some cases and false in others
Explanation
When solving for a point where the function will be undefined, you set the denominator equal to zero and solve for . This creates a vertical asymptote because when the denominator equals zero the function is undefined and we are solving for
. Say for example a function is undefined at
. So at all values of
where
this function is undefined creating a vertical asymptote.
True or False: For the inequality 


True
False
Explanation
This inequality wants all values where 


Which of the following best describes the statement:
The undefined points of rational functions are vertical asymptotes.
The statement is always true
The statement is always false
The statement is true in some cases and false in others
Explanation
When solving for a point where the function will be undefined, you set the denominator equal to zero and solve for . This creates a vertical asymptote because when the denominator equals zero the function is undefined and we are solving for
. Say for example a function is undefined at
. So at all values of
where
this function is undefined creating a vertical asymptote.
Solve and graph:
Explanation
Graph the rational expression,
-
Because
and a divide by
is undefined in the real number system, there is a vertical asymptote where
.
-
As
,
, and as
,
.
-
As
,
, and as
,
.
-
The funtion y is exists over the allowed x-intervals:
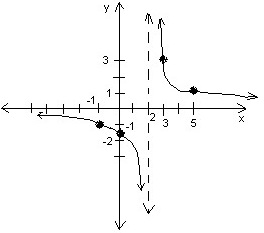
One approach for solving the inequality:
For
-
Determine where
over the x-values
or
.
-
for the intervals
or
.
-
Then the solution is
.
Another approach for solving the inequality:
- Write
as
, then determine the x-values that cause
to be true:

-
is true for
or
.
-
Then the solution is
.
Explanation
The zeros of the function are the values of 
We only need to solve for 
So the zeros of this function are 
To solve for the points at which this function will be undefined, we set the denominator equal to zero and solve for 
Solve the inequality.
Explanation
First, subtract 

Then find the common denominator and simplify

Next, factor out the numerator
and set each of the three factor equal to zero and solve for 
The solutions are

Now plug in values between 
![\left(-1,\frac{1}{3}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462780/gif.latex)
![\left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462781/gif.latex)

Note that 

![\left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462782/gif.latex)
Thus, the solution to the inequality is
![(-\infty ,-1)\cup \left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462783/gif.latex)
Solve the inequality.
Explanation
First, subtract 

Then find the common denominator and simplify

Next, factor out the numerator
and set each of the three factor equal to zero and solve for 
The solutions are

Now plug in values between 
![\left(-1,\frac{1}{3}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462780/gif.latex)
![\left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462781/gif.latex)

Note that 

![\left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462782/gif.latex)
Thus, the solution to the inequality is
![(-\infty ,-1)\cup \left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462783/gif.latex)
Explanation
The zeros of the function are the values of 
We only need to solve for 
So the zeros of this function are 
To solve for the points at which this function will be undefined, we set the denominator equal to zero and solve for 


























![[-\infty, 2] \cup [5, +\infty ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/294387/gif.latex)
![[2, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/477836/gif.latex)




















 , undefined:
, undefined: 









![(-\infty ,-1)\cup \left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462777/gif.latex)
![\left(-1,\frac{1}{3}\right]\cup [2,\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462778/gif.latex)

![\left(-\infty ,\frac{1}{3}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462779/gif.latex)

