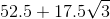All High School Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Right Triangle
What is the perimeter of a triangle with side lengths of 5, 12, and 13?
To find the perimeter of a triangle you must add all of the side lengths together.
In this case our equation would look like
Add the numbers together to get the answer 
Example Question #1 : How To Find The Perimeter Of A Right Triangle
Three points in the xy-coordinate system form a triangle.
The points are 
What is the perimeter of the triangle?
Drawing points gives sides of a right triangle of 4, 5, and an unknown hypotenuse.
Using the pythagorean theorem we find that the hypotenuse is 
Example Question #171 : Triangles
Find the perimeter of the following triangle:

The formula for the perimeter of a right triangle is:
where 
Use the formulas for a a 


Our 
Plugging in our values, we get:
Example Question #84 : Right Triangles
Find the perimeter of the following right triangle:

The formula for the perimeter of a right triangle is:
where 
Use the formulas for a 

Our 
Plugging in our values, we get:
Example Question #2 : How To Find The Perimeter Of A Right Triangle

Based on the information given above, what is the perimeter of triangle ABC?
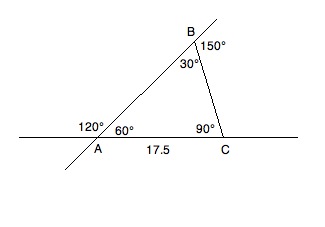
Consult the diagram above while reading the solution. Because of what we know about supplementary angles, we can fill in the inner values of the triangle. Angles A and B can be found by the following reductions:
A + 120 = 180; A = 60
B + 150 = 180; B = 30
Since we know A + B + C = 180 and have the values of A and B, we know:
60 + 30 + C = 180; C = 90
This gives us a 30:60:90 triangle. Now, since 17.5 is across from the 30° angle, we know that the other two sides will have to be √3 and 2 times 17.5; therefore, our perimeter will be as follows:
All High School Math Resources