All High School Math Resources
Example Questions
Example Question #201 : Triangles
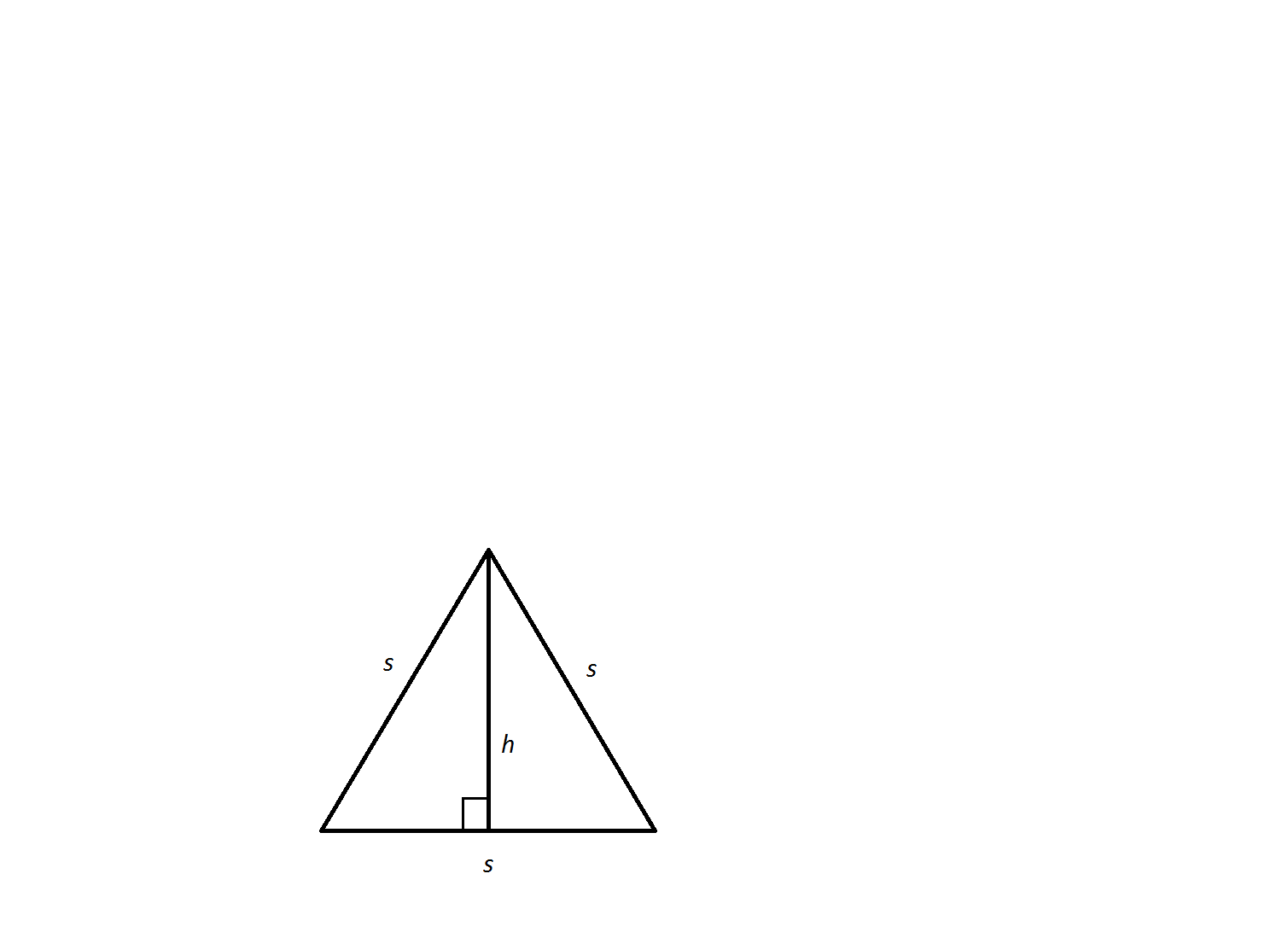
An equilateral triangle has a side length of 

Not enough information to solve
The altitude, 

In a 






In this scenario:
and
Therefore,

Example Question #202 : Triangles

An equilateral triangle has a side length of 

Not enough information to solve
An altitude slices an equilateral triangle into two 



Therefore, we can find the height of the altitude of this triangle by designating a value to 



Example Question #481 : Geometry
What is the height of an equilateral triangle with side 6?
When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the 

Example Question #211 : Triangles
Find the height of the following equilateral triangle:
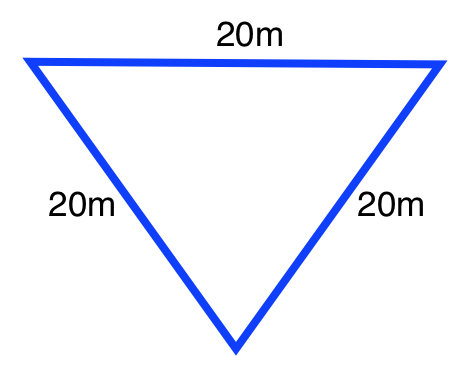
Each angle in an equilateral triangle is 
Use the formula for 
The formula is:
Where 
If we were to create a 



Example Question #212 : Triangles
Solve for the value of X in the following equilateral triangle:
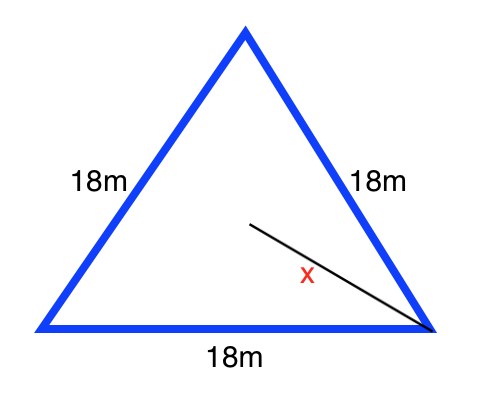
If we draw a line segment between X and the base of the triangle, we form a 
We can use the relationships between the sides of a 
We know the base opposite the 

The value of the height opposite the 


Therefore, the value of X will be twice the value of the height:
Example Question #1 : How To Find The Height Of An Equilateral Triangle
What is the height of an equilateral triangle with a side length of 8 in?
An equilateral triangle has three congruent sides, and is also an equiangular triangle with three congruent angles that each meansure 60 degrees.
To find the height we divide the triangle into two special 30 - 60 - 90 right triangles by drawing a line from one corner to the center of the opposite side. This segment will be the height, and will be opposite from one of the 60 degree angles and adjacent to a 30 degree angle. The special right triangle gives side ratios of 



The side with length 

Certified Tutor
Certified Tutor
All High School Math Resources










































