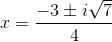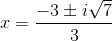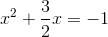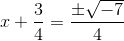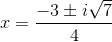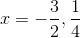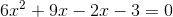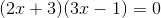All High School Math Resources
Example Questions
Example Question #41 : Quadratic Equations And Inequalities
Solve the following equation using the quadratic form:
Factor and solve:

or
This has no solutions.
Therefore there is only one solution:
Example Question #21 : Solving Quadratic Equations
Solve the following equation using the quadratic form:
Factor and solve:

or
Therefore the equation has four solutions:
Example Question #26 : Solving Quadratic Equations
Solve the following equation using the quadratic form:
Factor and solve:

or
Therefore the equation has two solutions.
Example Question #43 : Quadratic Equations And Inequalities
Solve the following equation using the quadratic form:
Factor and solve:
Each of these factors gives solutions to the equation:
Example Question #51 : Quadratic Equations And Inequalities
The product of two consecutive positive numbers is 
Let 

The equation to sovle becomes 

Factoring we get 




Example Question #29 : Solving Quadratic Equations
Two positive, consecutive odd numbers have a product of 
Let 

Use the distributive property and subtract 

Factoring we get 
Solving we get 

The problem stated that the numbers were positive so the answer becomes 
Example Question #332 : Algebra Ii
Find the sum of the solutions to:
Multiply both sides of the equation by 
This can be factored into the form
So we must solve

and
to get the solutions.
The solutions are:
and their sum is 
Example Question #1 : Completing The Square
Find the vertex of the parabola by completing the square.
To find the vertex of a parabola, we must put the equation into the vertex form:
The vertex can then be found with the coordinates (h, k).
To put the parabola's equation into vertex form, you have to complete the square. Completing the square just means adding the same number to both sides of the equation -- which, remember, doesn't change the value of the equation -- in order to create a perfect square.
Start with the original equation:
Put all of the 
Now we know that we have to add something to both sides in order to create a perfect square:
In this case, we need to add 4 on both sides so that the right-hand side of the equation factors neatly.
Now we factor:
Once we isolate 
Thus, the parabola's vertex can be found at 
Example Question #2 : Completing The Square
Complete the square:
Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Example Question #3 : Completing The Square
Use factoring to solve the quadratic equation:
Factor and solve:
Factor like terms:
Combine like terms:
All High School Math Resources






































































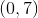

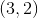

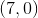
![\small f(x)=a[b(x-h)]^{2}+k](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/108179/gif.latex)




%5E%7B2%7D)