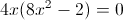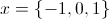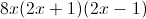All High School Math Resources
Example Questions
Example Question #1 : Simplifying Polynomials
Simplify the following polynomial:
To simplify the polynomial, begin by rearranging the terms to have positive exponents:
Now, combine like terms:
Simplify the integers:
Example Question #251 : Algebra Ii
Simplify the following polynomial:
Begin by reversing the numerator and denominator so that the exponents are positive:
Square the right side of the expression and multiply:
Simplify:
Example Question #261 : Algebra Ii
Simplify the following polynomial:
Begin by simplifying the integers:
Subtract the exponent in the denominator from the exponent in the numerator:
Example Question #11 : Polynomials
Simplify the following polynomial:
Begin by multiplying the terms:
Convert into fraction form:
Example Question #263 : Algebra Ii
Simplify the following polynomial:
Use the FOIL method to multiply the terms: F (first) O (outer) I (inner) L (last)
Example Question #264 : Algebra Ii
Simplify the following polynomial:
Use the FOIL method to multiply the terms: F (first) O (outer) I (inner) L (last)
Combine like terms:
Example Question #11 : Intermediate Single Variable Algebra
If 





Example Question #1 : Factoring Polynomials
Factor
Cannot be Factored
Use the difference of perfect cubes equation:
In 

Example Question #2 : Factoring Polynomials
Factor the polynomial completely and solve for 
To factor and solve for 
Factor 
Use the "difference of squares" technique to factor the parenthetical term, which provides the completely factored equation:
Any value that causes any one of the three terms 



Example Question #1 : Factoring Polynomials
Factor the following expression:
You can see that each term in the equation has an "x", therefore by factoring "x" from each term you can get that the equation equals 
All High School Math Resources
































































![b=\sqrt[3]{64}=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/94643/gif.latex)