All GMAT Math Resources
Example Questions
Example Question #1 : Dsq: Calculating Whether Right Triangles Are Congruent
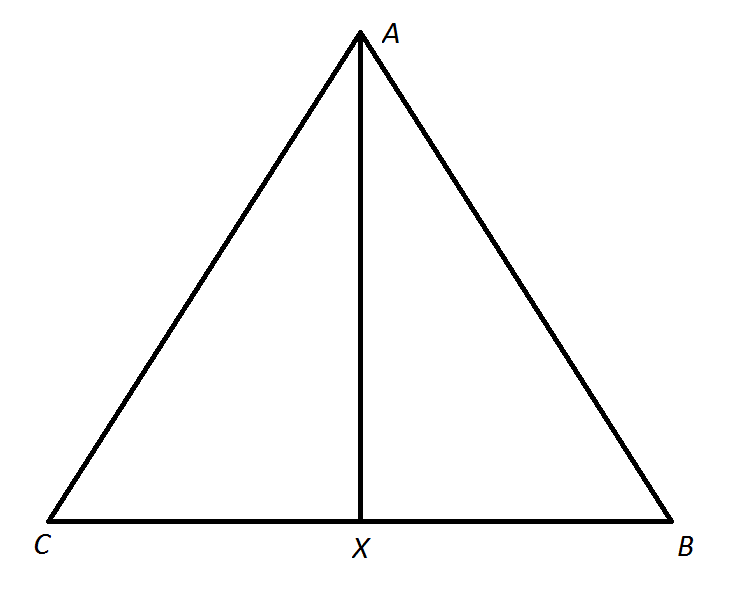
Note: Figure NOT drawn to scale.
Refer to the above diagram.
True or false:
Statement 1: 
Statement 2: 

Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
To prove triangle congruence, we need to establish some conditions involving side and angle congruence.
We know 
If we only assume Statement 1, then we know that 


Example Question #1 : Dsq: Calculating Whether Right Triangles Are Congruent
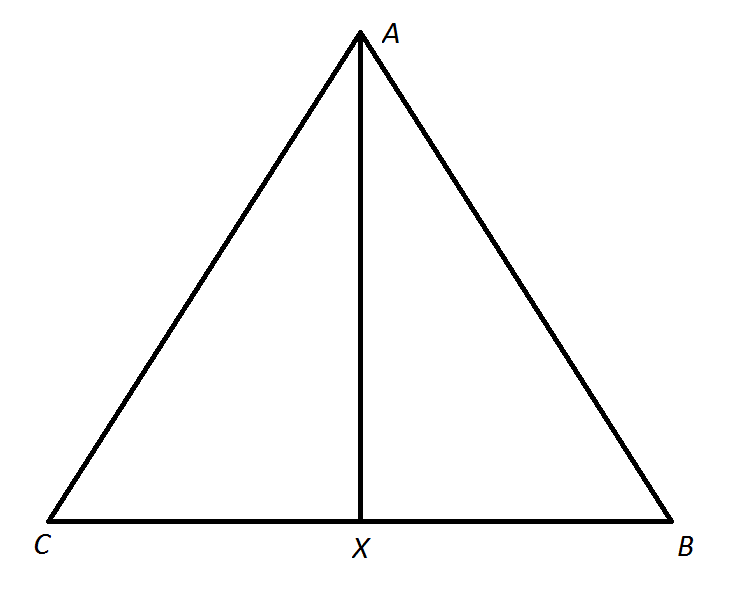
Note: Figure NOT drawn to scale.
Refer to the above diagram.
True or false:
Statement 1: 

Statement 2: 

BOTH statements TOGETHER are insufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
To prove triangle congruence, we need to establish some conditions involving side and angle congruence.
We know 
From Statement 1 alone, by definition, 




From Statement 2 alone,we know that 
Example Question #1 : Right Triangles
Given: 

True or false: 
Statement 1:
Statement 2:
BOTH statements TOGETHER are insufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Assume Statement 1 alone. If 



Now assume both statements to be true.
Suppose 

Similarly, if 

and 



Example Question #2 : Right Triangles
Given: 

True or false: 
Statement 1: 
Statement 2:
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
From Statement 1 alone, we are only give one angle congruency and one side congruency, which, without further information, is not enough to prove or to disprove triangle congruence. By a similar argument, Statement 2 alone is not sufficient either.
Assume both statements are true. By Statement 1, the hypotenuses are congruent, and by Statement 2, one pair of corresponding legs are congruent. These are the conditions of the Hypotenuse Leg Theorem, so 
Example Question #5 : Dsq: Calculating Whether Right Triangles Are Congruent
Given: 

True or false: 
Statement 1:
Statement 2:
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Each statement alone give information about only one of the triangles; without information about the other triangle, it is impossible to prove or to disprove triangle congruence.
Assume both statements are true. For 













Example Question #6 : Dsq: Calculating Whether Right Triangles Are Congruent
Given: 

True or false: 
Statement 1: 

Statement 2:
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Assume both statements to be true.



This establishes that 
Example Question #7 : Dsq: Calculating Whether Right Triangles Are Congruent
Given: 

True or false: 
Statement 1:
Statement 2:
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Assume Statement 1 only. By the Pythagorean Theorem, 




Assume Statement 2 only. By the Pythagorean Theorem, 


The two statements together, however, are sufficient. Statements 1 and 2 estabish congruence between the hypotenuses and corresponding legs, respectively, setting up the conditions of the Hypotenuse-Leg Theorem. As a consequence, 
Example Question #8 : Dsq: Calculating Whether Right Triangles Are Congruent
Given: 

True or false: 
Statement 1:
Statement 2:
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
In any right triangle, the hypotenuse must have length greater than either leg. Therefore, 

Assume Statement 1 alone. For 






Example Question #9 : Dsq: Calculating Whether Right Triangles Are Congruent
Given: 

True or false: 
Statement 1: 

Statement 2:
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
Assume Statement 1 alone. In any right triangle, the two acute angles are complementary. Therefore, 









Assume Statement 2 alone. If 




Example Question #1 : Right Triangles
Given: 

True or false: 
Statement 1:
Statement 2:
BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Assume both statements are true. Statement 1 establishes that 


All GMAT Math Resources




























