All GMAT Math Resources
Example Questions
Example Question #21 : Quadrilaterals
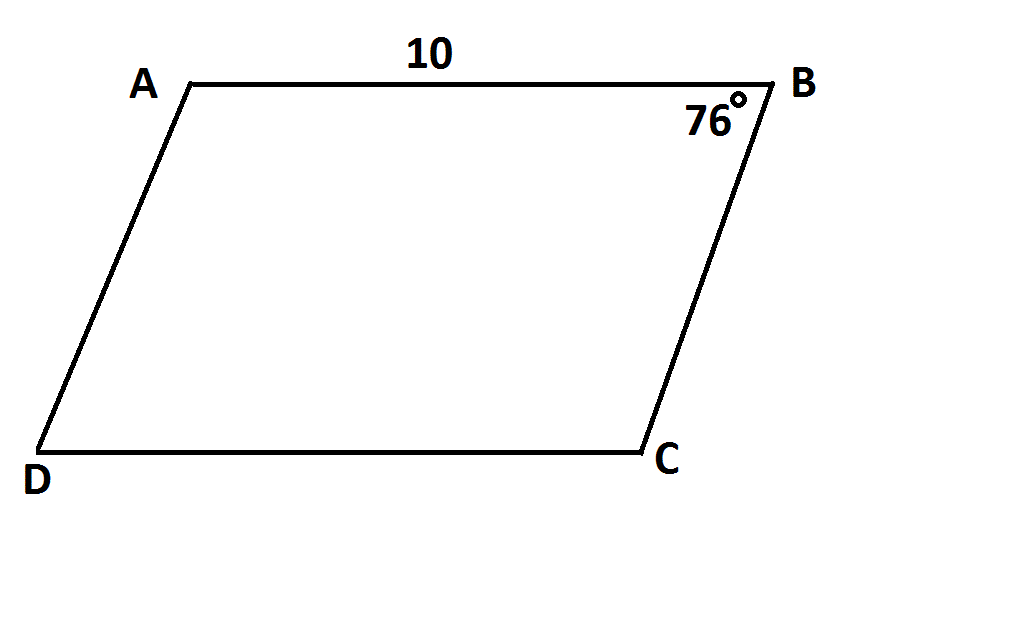
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
BOTH statements TOGETHER are insufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Example Question #181 : Data Sufficiency Questions

Notes: 
Calculate 
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Consider the area formula for a trapezoid:


So, if you know both the area and 
Example Question #181 : Data Sufficiency Questions
Consider parallelogram 
I) The perimeter of 

II) Side 


Find the length of side 
Both statements are needed to answer the question.
Statement I is sufficient to answer the question, but statement II is not sufficient to answer the question.
Neither statement is sufficient to answer the question. More information is needed.
Either statement is sufficient to answer the question.
Statement II is sufficient to answer the question, but statement I is not sufficient to answer the question.
Both statements are needed to answer the question.
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
Example Question #4 : Dsq: Calculating The Length Of The Side Of A Quadrilateral
Calculate the side of a square.
Statement 1: A circle with an area of 
Statement 2: A circle with a circumference of 
Statement 1: A circle with an area of 
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of 
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
Example Question #182 : Data Sufficiency Questions
Consider isosceles trapezoid 
I) 

II) The larger base of 
Find the length of the two legs of 
Statement I is sufficient to answer the question, but Statement II is not sufficient to answer the question.
Statement II is sufficient to answer the question, but Statement I is not sufficient to answer the question.
Either statement is sufficient to answer the question.
Neither statement is sufficient to answer the question. More information is needed.
Both statements are needed to answer the question.
Neither statement is sufficient to answer the question. More information is needed.
Consider isosceles trapezoid 
I) 

II) The larger base of 
Find the length of the two legs of 
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of 
Statement II relates the two bases of 
We are told that 
We still have three unknowns and two equations, so we cannot solve this system of equations.
All GMAT Math Resources




















