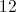All Calculus 1 Resources
Example Questions
Example Question #1 : How To Find Velocity
If during the first 15 seconds of its flight the displacement of a spacecraft is given by the equation 21.25x + x2 feet, what is its velocity at 10 seconds, given that its initial velocity is 0?
21.25 + 20 feet/second
1.25 * 212.5 * log(2) + 20 feet/second
None of the other answers
1.25 * 212.5 * log(2) + 100 feet/second
1.25 * 212.5 + 20 feet/second
1.25 * 212.5 * log(2) + 20 feet/second
To find the velocity function based on displacement, use the first derivative of f(x) = 21.25x + x2. f'(x) = 1.25 * ln(2) * 21.25x + 2x
The velocity at x = 10 would therefore be: f'(10) = 1.25 * log(2) * 21.25 * 10 + 2 * 10 = 1.25 * 212.5 * log(2) + 20 feet/second
Example Question #1 : How To Find Velocity
What is the instantaneous velocity at time t = π/2 of a particle whose positional equation is represented by s(t) = 12tan(t/2 + π)?
3√2
6√2
12
6
12√2
12
The instantaneous velocity is represented by the first derivative of the positional equation.
v(t) = s'(t) = 12 * (1/2) sec2(t/2 + π) = 6sec2(t/2 + π) = 6/cos2(t/2 + π) = 6/((–1)2 cos2(t/2)) = 6/cos2(t/2)
Based on the nature of the cosine, we know that 6/cos2(t/2 + π) = 6/((–1)2 cos2(t/2)) = 6/cos2(t/2)
To solve, v(π/2) = 6/cos2(t/2) = 6/((1/√2)2) = 6/(1/2) = 12
Example Question #2 : Spatial Calculus
What is the instantaneous velocity at time t=π/2 of a particle whose positional equation is represented by s(t) = 12cos2(t/2 + π)?
0
2√3
–6
–12
2
–6
The instantaneous velocity is represented by the first derivative of the positional equation. This is found by using the chain rule both on the square of the cosine function and the function itself.
v(t) = s'(t) = 12 * 2 cos(t/2 + π) * (–sin(t/2 + π)) * (1/2) = –12cos(t/2 + π)sin(t/2 + π)
Given what we know about the cosine and sine functions, we know cos(t/2 + π) = –cos(t/2) and sin(t/2 + π) = –sin(t/2)
Therefore, v(t) = –12(–sin(t/2))(–cos(t/2)) = –12sin(t/2)cos(t/2)
v(π/2) = –12sin(π/4)cos(π/4) = –12(1/√2)(1/√2) = –12 * (1/2) = –6
Example Question #3 : Calculus
A weight hanging from a spring is stretched down 3 units beyond its rest position and released at time t=0 to bob up and down. Its position at any later time t is
What is its velocity at time 
Example Question #1 : How To Find Velocity
The position 


The velocity function is given by the derivative of the position function. So here 

Example Question #1 : Derivatives
The position of a particle is given by 

The velocity is given as the derivative of the position function, or

We can use the quotient rule to find the derivative of the position function and then evaluate that at 
![\left[\frac{f(x)}{g(x)}\right]'=\frac{g(x)f'(x)-f(x)g'(x)}{[g(x)]^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/131451/gif.latex)
In this case, 

We can now substitute these values in to get
![\left[\frac{f(t)}{g(t)}\right]'=\frac{(t+1)*(4t)-(2t^2+1)*(1)}{(t+1)^2}=\frac{2t^2+4t-1}{(t+1)^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90777/gif.latex)
Evalusting this at 

So the answer is 
Example Question #3 : Calculus
Find the velocity function if the position function is given as: 
There are three terms in this problem that has to be derived. The derivative of the position function, or the velocity function, represents the slope of the position function.
The derivative of 
Therefore. the derivative of 

The derivative of 

The derivative of 

Example Question #4 : Calculus
Find the velocity function given the position function: 
The derivatives can be solved term by term.
First, find the derivative of 
Find the derivative of 

Therefore, the velocity function is:
Example Question #5 : Calculus
Find the velocity of a function if the acceleration is: 
To find the velocity given the acceleration function, we will need to integrate the acceleration function.
Example Question #10 : Velocity
Find the velocity at 

The velocity function can be obtained by integrating the acceleration function.
Since we are finding the velocity at 
Certified Tutor
All Calculus 1 Resources