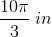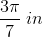All Basic Geometry Resources
Example Questions
Example Question #1 : How To Find The Distance Between Clock Hands
The minute hand of a clock is exactly six inches in length, and the tip of the minute hand has traveled exactly ten inches since noon. To the nearest minute, what time is it?
12:16
12:28
12:08
12:44
12:32
12:16
The path traveled by the tip of the minute hand over the course of one hour is a circle of radius 

The tip has traveled 10 inches since noon, so the fraction of the circle traveled is 
and the number of minutes that have expired since noon is 
Therefore, to the nearest minute, the time is 12:16.
Example Question #1 : How To Find The Distance Between Clock Hands
What is the distance, in minutes and seconds, between the minute and hour hands of a clock at 
The clock face is divided into sixty equal parts, each minute. The minute hand is located on the 20 minute mark at 6:20, the hour hand located between the 30 minute mark and the 35 minute mark. When the minute hand goes all sixty minutes, the hour hand only moves five, so to figure out the location of the hour hand, we look at how much the hour has progressed, in this case 20 minutes, or one third of the hour. So the minute hand has moved one third of the way through the hour, so has the hour hand moved one third of the way through the five minutes, or, five thirds of a minute, which is one and two thirds minute, one minute forty seconds. That puts the hour hand at thirty minutes plus one minute and forty seconds—at 31min 40sec—which is 11min 40sec farther than the minute hand.
Example Question #3 : How To Find The Distance Between Clock Hands
Which pair of hands is further apart and by how much? Clock A is pointing at 

B's hand are further apart by
B's hands are further apart by
A's hands are further apart by
A's hands are further apart by
A's hands are further apart by
The distance between A's hands is simple to find, the minute hand is on the 6 at 30 minutes, halfway through the hour and the hour hand is resting just past the 3 at 15 minutes. What the minute hand travels in an hour, the hour hand travels in five minutes, so halfway through five minutes is 
To find the distance we subtract 17.5 from 30:
Therefore A's hands have a 12.5 minutes distance.
The distance between B's hands is the same procedure, the minute hand is on the 7 at 35 minutes, 35/60 through the hour, and the hour hand is resting past the 4 at 20 minutes, so 
putting B's hands 12 minutes apart.
Example Question #4 : How To Find The Distance Between Clock Hands
Find the distance between the clock hands when the time is 








The first thing you will have to do is determine the degrees that the hour hand is away from the minute hand. To help find the degrees of the hour and minute hand, you have to realize that when the minute hand is at 30 minutes, the hour hand is halfway between the hours of 10 and 11. Using the fact that at 9:00, the hour and minute hands create a 


Using the degrees and the circumference of a circle, you can find the distance of the arc length with the following formula.
where,
The minute hand represents our radius therefore 
Therefore, our equation becomes:
Example Question #2 : How To Find The Distance Between Clock Hands
A certain clock has a minute hand 12 cm long and an hour hand that is 9 cm long. At 9:00, how far apart are the ends to the two hands of the clock?
A picture will help a bunch for this problem, so we begin by looking at a clock at 9:00

We should notice two things. The first is that by drawing in the distance we wish to find, namely that between the ends of the two hands, we end up with a triangle. Secondly, remembering that a full circle is 360 degrees, we see that the distance between the two hands spans 3 hours, or one fourth of the circle. One fourth of 360 is 90, so the angle between our two hands is a right angle.

We now realize that we have a right triangle, and our desired distance is simply the hypotenuse, which we can name 
Taking the square root gives our answer.
Example Question #43 : Plane Geometry
A clock has two equally long hands on it, each measuring 


Our clock looks roughly like this:

Now, between every number on the clock, there are 




Now, we know:
We know that 
Example Question #1235 : Gre Quantitative Reasoning
A clock has two equally long hands on it, each measuring 


Our clock looks roughly like this:

Now, between every number on the clock, there are 





Now, we know:
We know that 
Example Question #384 : Plane Geometry
A clock has two equally long hands on it, each measuring 



Our clock looks roughly like this:

Now, between every number on the clock, there are 










Now, we know:
We know that 
All Basic Geometry Resources