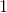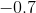All AP Statistics Resources
Example Questions
Example Question #272 : Ap Statistics
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Histogram
Scatterplot
Bar chart
Z-score
Bell curve
Scatterplot
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Example Question #273 : Ap Statistics
Based on the scatter plot below, is there a correlation between the 

Yes; negative linear relationship
Yes; positive linear relationship
No; there is no correlation
Yes; negative exponential relationship
Yes; negative linear relationship
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
Example Question #2 : Graphing Data
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)







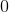


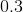


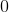


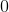
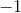



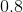
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

Example Question #274 : Ap Statistics
Find the range of the data in the stem-and-leaf plot.
To find the range, subtract the minimum value from the maximum value
minimum:
maximum:
So,
maximum - minimum =
Example Question #1 : How To Interpret Stemplots
Find the median of the stem and leaf plot.
The median is the middle value of the set in increasing order.
In this set of 11 entries, the median is the 6th entry of the set in increasing order, or 26.
Example Question #2 : How To Interpret Stemplots
How many entries are in this stem and leaf plot?
The number of entries is the number of digits on the right hand side of the column.
Since there are 21 total digits, there are 21 total entris that make up the stem and leaf plot.
Example Question #4 : How To Interpret Stemplots
What is the interquartile range of the following data set?

This stemplot is read as follows: the stem is the tens digit and each digit in the "leaves" section is a ones digit. Put them together to have a data point.
53, 65, 68, 69, 70, 72, 72, 79, 83, 84, 85, 87, 89, 90, 94
In the particular case there are 15 data points therefore the median is 79. Thus the first quartile is 69 and the third quartile is 87.
Finding the interquartile range is subtracting the first quartile from the 3rd quartile.
Example Question #1 : How To Interpret Histograms
Based on the histogram, which of the following sets of values was most common in the sample?
64-70
62-68
58-64
54-60
66-72
62-68
You can see from the histogram that the two most frequent ranges for values are 62-64 and 64-66, with 5 values in each group. And from the answer choices, you should see that only one choice, 62-68, contains both of the high-frequency bars. It also contains the next-highest bar (66-68, with a total of 4), so at 14 total values the range 62-68 has the highest frequency of any of these six-inch-range sets in the choices.
Example Question #2 : How To Interpret Histograms
What is the best measurement of center and spread for the following data set represented by a histogram?

Mean and Standard Deviation
Mean and Interquartile Range
Median and Interquartile Range
Median and Standard Deviation
Mean and Range
Median and Interquartile Range
For skewed distributions, the outliers can greatly affect the value of the mean and the standard deviation. Therefore, the median and IQR would be better measures of center and spread because they are not greatly influenced by outlier values.
Example Question #1 : How To Interpret Histograms
Louie collects data on the amount of sleep students in his class get.
Below is a graphical representation of the data

Which of the following is/are false about Louie's class' data?
i: the student with 2 hours of sleep is an outlier
ii: without the student with 2 hours of sleep the data is roughly normally distributed
iii: without the student with 2 hours of sleep the data is slightly right skewed
iv: the student with 2 hours of sleep is within 2 standard deviations of the mean
i & ii
i, ii & iii
ii & iv
ii, iii & iv
iii & iv
ii & iv
Entering the data into a calculator you can quickly find the mean to be 6.5 and the sd to be 1.6 6.5-3.2=3.3 3.3>2 so iv is false and by virtue of this 2 is an outlier so i is true.
Between ii and iii, the data is not bell shaped, and does exhibit a slight right skew without the mentioned pt due to more density on 5 and 6 hours than 8 and 9
Certified Tutor
All AP Statistics Resources