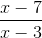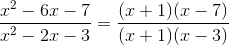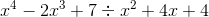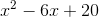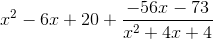All ACT Math Resources
Example Questions
Example Question #1 : How To Divide Trinomials
Simplify the expression:
Once simplified, (x+1) appears on both the numerator and denominator, meaning we can cancel out both of them.
Which gives us:
Example Question #2 : How To Divide Trinomials
Divide:

The set up would look very similar to the division of real numbers, such as when we want to divide 10 by 2 and the answer is 5.
The first step after setting up the "division house" is to see what the first term in the outer trinomial needs to multiplied by to match the 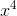


While we could continue to divide, it would require the use of fraction exponents that would make the answer more complicated. Therefore, the term in red will be the remainder. Because this remainder is still subject to be being divided by the trinomial outside of the division house, we will make the remainder part of the final answer by writing it in fraction form:
Therefore the final answer is
Example Question #1 : How To Factor A Polynomial
Which of the following is a factor of the polynomial 3y2+14y-24?
y-6
4y-3
3y+4
y+6
3y-6
y+6
The polynomial factors to (3y-4)(y+6). (y+6) is the only one of those two options available as an answer.
Example Question #2 : How To Factor A Polynomial
Factor the polynomial : x3 + 27
(x +3) (x2 - 3x +9)
(x2 + 3) (x – 3x +9)
(x +9) (x2 - 3x +9)
(x +3) (x2 - 3x +3)
(x +3) (x2 - 3x +9)
First, write as a sum of the cubes,
x3 + 33, then factor : (x + 3) (x2 – 3x + 32). Apply the exponent:
(x + 3) (x2 – 3x + 9)
Example Question #3 : How To Factor A Polynomial
Factor the polynomial: 2x2 + ab – 2b – ax2
(b - X2) (a + 2)
(x2 – 2) (a – b)
(x2 + b) (a - 2)
(x2 – b) (2 - a)
(x2 – b) (2 - a)
2x2 + ab – 2b – ax2 = 2x2 – 2b – ax2 + ab
Rearrange terms
= (2x2 – 2b) + (- ax2 + ab) Group
= 2(x2 – b) + a(-x2 + b) Factor each group
= 2(x2 – b) – a(x2 – b) Factor out -a
= (x2 – b) (2 – a) Factor out x2 – b
Example Question #4 : How To Factor A Polynomial
Which of the following is a factor of the polynomial 
Factor the polynomial by choosing two values that when FOILed will sum to the middle coefficient, 3, and multiply to 2. These two numbers are 1 and 2.
Only (x +1) is one of the choices listed.
Example Question #5 : How To Factor A Polynomial
Which of the following expressions is a factor of this polynomial?
The polynomial factors into the following expression:
Therefore, the answer is
Example Question #4 : How To Factor A Polynomial
Which of the following is equivalent to 
You have two options for a problem like this. On the one hand, you can merely FOIL the answers until you find one that equals the value given in the equation. The other option is to factor it adequately from the beginning. This is not too hard. Since the middle term is so small, you know that the numeric portions of your factors will have to be nearly equal. Since we know that 
Thus, your answer is:
Example Question #7 : Factoring Polynomials
Which of the following is equivalent to 
This cannot be factored.
You have two options for a problem like this. On the one hand, you can merely FOIL the answers until you find one that equals the value given in the equation. The other option is to factor it adequately from the beginning. For a question like this, it is a bit harder, given that there is a number in front of the first term. Now, given the signs in the original problem, you know that your groups will look like the following:
Now, you can do a little trick to make your life easier. Factor out the common 
The latter is very easy to factor:
Now, you have:
You can distribute the 
Example Question #8 : Factoring Polynomials
Which of the following is equivalent to 
You have two options for a problem like this. On the one hand, you can merely FOIL the answers until you find one that equals the value given in the equation. The other option is to factor it adequately from the beginning. This is not too hard. You know that your groups will need to have one positive and one negative between them (this is because of the 








Certified Tutor
Certified Tutor
All ACT Math Resources