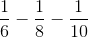How to find if right triangles are similar
Help Questions
SSAT Upper Level Quantitative › How to find if right triangles are similar
If a 

Explanation
For the triangles to be similar, the dimensions of all sides must have the same ratio by dividing the 3-4-5 triangle.
The 6-8-10 triangle will have a scale factor of 2 since all dimensions are doubled the original 3-4-5 triangle.
The only correct answer that will yield similar ratios is the 
The other answers will yield different ratios.
What is the main difference between a right triangle and an isosceles triangle?
A right triangle has to have a 

An isosceles triangle has to have a 

A right triangle has to have a 

A right triangle has to have a 

A right triangle has to have a 

Explanation
By definition, a right triangle has to have one right angle, or a