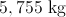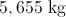All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Volume Of A Sphere
A car dealership wants to fill a large spherical advertising ballon with helium. It can afford to buy 1,000 cubic yards of helium to fill this balloon. What is the greatest possible diameter of that balloon (nearest tenth of a yard)?
The volume of a sphere, given its radius, is
Set 

The diameter is twice this, or 12.4 yards.
Example Question #2 : How To Find The Volume Of A Sphere
The diameter of a sphere is 

The diameter of a sphere is 
The volume enclosed by a sphere is given by the formula:

Example Question #3 : How To Find The Volume Of A Sphere
A spherical balloon has a diameter of 10 meters. Give the volume of the balloon.
The volume enclosed by a sphere is given by the formula:
where 

Example Question #1 : Volume Of A Three Dimensional Figure
The volume of a sphere is 1000 cubic inches. What is the diameter of the sphere.
The volume of a sphere is:
Where 


So we can get:
Example Question #181 : Geometry
A sphere has a diameter of 





To find the volume of a sphere, use the following formula:


Now, because we are given the diameter of the sphere, divide that value in half to find the radius.

Now, plug this value into the volume equation.


Example Question #4 : Volume Of A Three Dimensional Figure
What is the volume of a sphere with a diameter of 
Write the formula for the volume of the sphere.
The radius is half the diameter, which is five. Substitute the value.
Example Question #4 : How To Find The Volume Of A Sphere
What is the volume of a sphere with diameter 12 feet?
None of the other answers are correct
The radius of the sphere is half the diameter, or 6 feet; use the formula

Setting 
Example Question #161 : Geometry
Chestnut wood has a density of about 
First, convert the dimensions to cubic centimeters by multiplying by 


Its volume is found by using the formula and the converted height and radius.
Now multiply this by 
Finally, convert the answer to kilograms.
Example Question #3 : Volume Of A Three Dimensional Figure
A cone has the height of 4 meters and the circular base area of 4 square meters. If we want to fill out the cone with water (density = 
6333
The volume of a cone is:
where 

As the circular base area is 
where 
We know that density is defined as mass per unit volume or:
Where 


Example Question #1 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9
The vertical height (or altitude) of a right cone is 


The volume of a cone is:
where 

Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources









![r \approx \sqrt[3]{238.7} \approx 6.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92097/gif.latex)